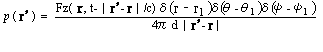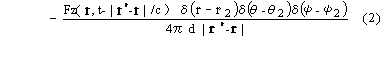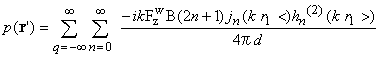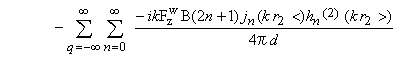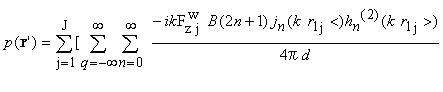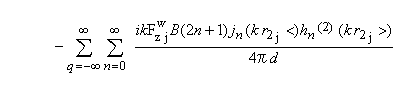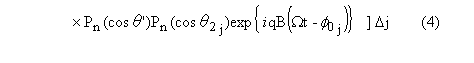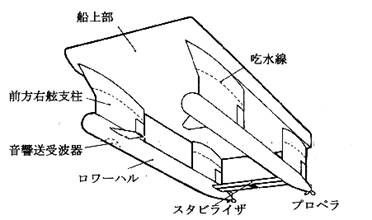
回転翼の発生音低減についての検討

1．はじめに　

海底地形の測量、海流情報の収集、火山噴火予知調査などの海洋調査をする船に，図１に示すような双胴船がある。この船は，二つのロワーハルにより船上部を水面から浮上させ航行するもので揺れや抵抗が少なく高速を出せる特徴を持つ。ロワーハル底部には，音響送受波器(あるいは送受波器アレイ)が付いており下方に音波を発信し海中／海底からの反射信号を受信する。例えば水深は，こうして測られた送受信における音波伝搬時間と音速から知られる。

このような観測システムにおいて，反射信号が十分に得られないといった状況が起きることがある。それは受信される信号に雑音が加わる場合である。この雑音は，主にロワーハル内の回転機械振動がハルを伝搬する固体音，ロワーハル後部に付くプロペラ発生音がハルに沿って伝搬する水中音，ハル周りに生じる乱流等の流体音，水中の散乱体による反射音等である。そして，こうした雑音に対してそれぞれ個別に，あるいは関連させて雑音低減対策が取られている。

この中で乱流などの流体音は高周波で著しく減衰する。一方プロペラ発生音は，翼枚数とプロペラ回転数の積の倍々の周波数で現れるため際限なく高周波まで雑音成分を持ち，いかなる周波数帯域で使用される音響機器に対しても雑音の要因となる。そこで，ここではそのプロペラ発生音の低減について検討する。プロペラ発生音には，キャビテーション，プロペラ翼の共振，推力変動によるものがある。キャビテーションが一番大きな雑音となり，キャビテーションが起きないような運転条件（船速の制限）や翼条件（プロペラの枚数や形状）など研究されている。そうした中で近年，複雑な形状のプロペラが工作できるようになった。その一つがスキュープロペラである。スキュープロペラによると発生音が小さくなると言われ，色々な船舶に使用されつつあるようである。

このスキュー翼にすることで,雑音がどれほど低減できるのであろうか?　ここでは海洋調査双胴船のロワーハルに付くプロペラのノンキャビテーションの状態における雑音低減に注目し，スキュー翼の発生音算出法を構築することを試みる。又本算出法を用いて，スキュー翼の実例を取り上げ実験で比較し算出法の妥当性を示すとともに騒音低減効果を明らかにする。

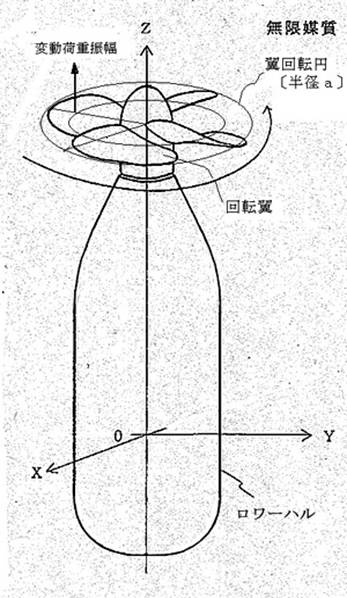
図2　ロワーハルモデルに

取り付けた回転翼

　図2にロワーハルモデルに取り付けた回転翼(プロペラを以後回転翼と呼ぶ)を示す。回転翼はロワーハル後部のウェーク(伴流)中で作動しており、1）低回転マッハ数で回転，2）ノンキャビテーションの状態，３）回転翼は同一形状・寸法の翼が円周方向に等間隔に分布の条件を置く。このような条件で，簡単な近似により発生音圧を求める公式^１)がある。それは，図に示すように回転翼それぞれ翼面上，単一の点で推力変動を考えこれを音源として発生音圧を求める算出法（ここでは翼面の単一荷重変動による音圧算出法と呼ぶ）である。しかし，一点にのみ音源を置くため実際翼面上に分布する音源の発生する音圧が必ずしも正確に得られない。正確には翼面上の音源分布を考慮しなければならず，翼そのものを反射体とする新たな解析〔翼形状に基づく音波回折などの計算〕が必要となる。しかし，翼形状が複雑であると中々簡単ではない。

そこで第一ステップとして，面状の翼に代え細長い翼を考えることにする。厳密に言うと翼弦寸法〔翼スパン（翼付け根と翼端を結ぶ母線長を翼スパンと呼ぶ）に垂直な方向の寸法〕が対象周波数の波長以下の翼を考える。この場合，翼弦周りを音波が完全に回折するから翼そのものの反射を無視できる。つまり翼を考えなくて良い。

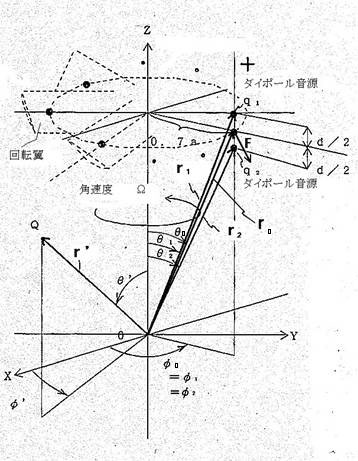
図3−１　翼面の単一荷重変動による音圧算出法の説明図

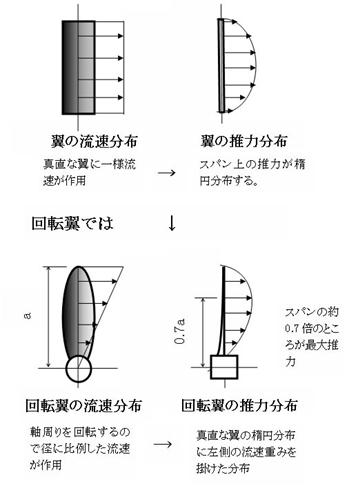
図3−１に直交座標ＸＹＺ上に取られた細長い回転翼における翼面の単一荷重変動による音圧算出法の説明図を示す。Ｚ軸からの偏角をθ,Ｘ軸からの偏角をφとする極座標(ｒ,θ,φ)を定義する。回転翼は，中心軸が直交座標ＸＹＺのＺ軸上にあり，Ｚ軸周りを角速度Ωで回転するものとする。ある一枚の翼で回転円半径ａの0.7倍の点の位置ベクトルをｒ_０，極座標で（r_０,θ_０,φ_０）とし，ここに翼に働く変動荷重Fを置く。この点は流体力学的に推力分布の最大を与える。図3−2に説明のため非回転翼の推力分布と回転翼の推力分布を示す。非回転翼では一様の流速が作用するときスパン上で推力が楕円分布することが知られている^２）。一方非回転翼では軸周りに翼が回転するのでスパン上の流速は図のように翼先端が一番速くなる。このときスパン上の推力は非回転翼の楕円分布する推力に回転翼の径方向に変化する流速の重みを掛けた分布となる。このときの推力最大点が図のような回転半径の0，７倍の所になるのである。単一荷重変動による音圧算出法では，この最大点に翼スパン上に分布する荷重の総和を集中させて考える。媒質中任意の点Ｑの位置ベクトルをｒ’とし極座標で(ｒ'，θ’，φ’)とする。

このとき，ノンキャビテーション，低回転マッハ数の仮定から点Qに発生する音圧は,Ｌｉｇｈｔｈｉｌｌの方程式の解^３）で体積変動による音圧と,４重極音源による音圧が無視でき荷重の変動による音圧として，

と示される。ただし，∇=ｅｘ∂/∂ｘ+ｅｙ∂/∂＋eｚ∂/∂ｚ　で，ex,ｅy,ｅzはそれぞれx,y,z方向の単位ベクトルである。またｃ：媒質中の音速，δ：ディラックのデルタ関数， t：時間である。ここでｒ_０は角速度Ωで変化する時間と空間の関数である。つまり時間の関数が空間の関数と分離できない。複数の翼が推力変動を受けて回転する場合，式(1)の形では荷重の遅延時間差が表せず，べッセル関数^４）による級数展開を用いて変数分離し遅延時間差を陽に表した公式が使われる^{１)，５），６）}。ただしこれは遠距離を仮定しており回転翼近傍のロワーハルの音波反射を考える場合には適用できない。ここでは，先ずこの問題を次節に示す単一ダイポール近似を用いて解決し近距離場でも適用できるような形に直すことにした。

図3−２　翼に働く推力分布の説明図

低回転マッハ数を考慮すると推力変動が優勢となる。そこで,式(１)中の∇でｅｚ∂/∂ｚの項のみを残す。更にここでは，式（1）のＺ軸方向の編微分を差分で近似する。このときｒ’における発生音圧は

となる。ここにFzはZ軸方向の変動推力である。r_１, r_２は図3−1において，それぞれ荷重点から上下にd／２離れたq_１，q_２の位置ベクトルであり、極座標でｑ_１(r_１，θ_１，φ_１)，ｑ_２〈r_２，θ_２，φ_２＝φ_１〉と示される。またｄは波長に比べて十分小さい値である。この式がダイポール音源を表し，回転翼の一点に近接して置かれた点ｑ_１，点ｑ_２の正負の強度を持つ二つの点音源の発生音圧の和として示される。

　さて式(２)に現れるｒ，ｒ₁およびr₂は角速度Ωで変化する時間と空間の関数で時間の関数が空間の関数と分離できない。この形では，後に普通翼やスキュー翼の発生音圧を論じる際，位相の干渉が式に明示できないので都合が悪い。そこで式(２)を球面状素波の重畳として時間及び空間の変数分離した級数展開式で表すことにする^{７），８)，９)，10)}。結果として得られるＢ枚の翼が発生する音圧を示すと，

　　　　　　　　　　　　　　　　　　（3）

である。ここに，ｉは虚数単位，ｒ₁＜：min（ｒ’，ｒ₁），ｒ₁＞：maｘ（ｒ’，ｒ₁），ｒ₂＜：min（ｒ’，ｒ₂），ｒ₂＞：max（ｒ’，ｒ₁）であり，jnはn次の第一種球ベッセル関数^９），ｈn^（２）はn次の第二種球ハンケル関数^９），Pnはn次の第一種ルジャンドル関数^９），φ₀は初期位相である。またqは高調波番号， F_z^Wは時間変動する推力をフーリエ級数に展開したときの高調波周波数ＷΩ（ただし，Ｗは高調波番号ｑと翼枚数Ｂの積）における推力成分であり，実測データあるいは回転翼の流体力学的相似モデルの推力時系列データをフーリエ展開すると求まる。ｋは波数で媒質中の音速ｃを用いてＷΩ／ｃと表される。式(３)から，音圧は時間と空間に関する変数分離された形で得られ，あらゆる高調波周波数ＷΩの音圧成分を含んだ広帯域な音圧となることが知られる。ここでは式(3)の形を単一ダイポール近似と呼ぶ。式（3）への展開

次に，この単一ダイポール近似による発生音圧算出式を基に，普通翼及びスキュー翼の発生音圧算出法を構築する。

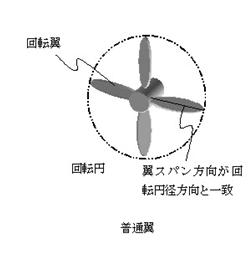
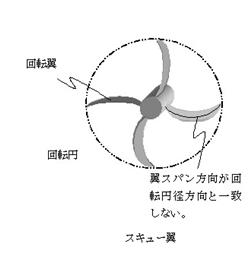
２．３　普通翼及びスキュー翼の発生音圧算出法の構築

図４に回転翼として使用される普通翼とスキュー翼を示す。普通翼は，回転翼のスパン方向が回転円の径方向と一致するような翼，これに対しスキュー翼は，回転翼のスパン方向が回転円の径方向と一致しない翼である。（実際には，わずかにスキューがついたものが多いが，ここではそれらの翼も回転円の径方向とほぼ一致するものとし普通翼と考える。）　このような、普通翼とスキュー翼についての発生音圧算出法を示す。

図４　普通翼とスキュー翼

図5　普通翼の分布ダイポールと単一

ダイポール近似の音源位置

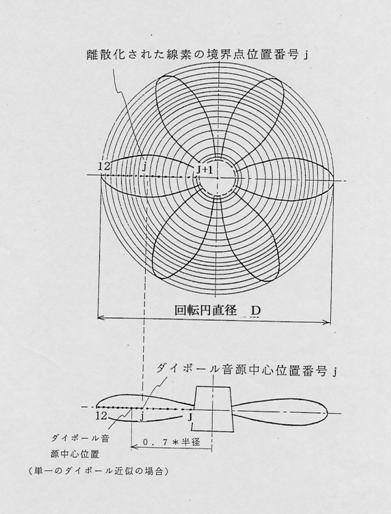
普通翼の発生音圧は以下のようにして求める。図5に普通翼の分布ダイポールと単一ダイポール近似の音源位置を示す。図に示すように翼経線方向を微小線素で分割する。ただしｊはダイポール音源を置く線素の中心位置番号，Jは全線素数である。このように離散化された線素ｊ上に未定の推力強さF_z^w_j（ただし，線素ｊにおける高調波周波数WΩにおける推力成分）を持つダイポールを置く。それぞれ中心位置番号ｊにおける強さは図3−2で示した回転翼の推力分布に従うものとする。そして定常状態で流体力学的に定まる所定の推力が単一ダイポール近似と普通翼で等しいとした未定の推力強さF_z^w_jに関する超越方程式を作る。これを解いて翼経線方向に分布したダイポールによる発生音圧の総和を計算する。式に示すと，

となる。ここでｒ_1ｊ,θ_1ｊ,ｒ_2ｊ,θ_2ｊは中心位置番号ｊにおけるダイポールの位置座標変数，φ_0ｊは中心位置番号ｊにおけるダイポールの初期位相，Δｊは中心位置番号ｊにおけるダイポールの微小線素を示す。またｒ_1ｊ＜：min（ｒ’，ｒ_1ｊ），ｒ_1ｊ＞：maｘ（ｒ’，ｒ_1ｊ），ｒ_2ｊ＜：min（ｒ’，ｒ_2ｊ），ｒ_2ｊ＞：max（ｒ’，ｒ_1ｊ）である。式(4)に注目すると普通翼の場合,ダイポール音源は経線上に分布するのでφ_0ｊ（ｊ＝１，・・Ｊ）は全て等しい。よって時間の関数項exp｛ｉｑＢ（Ωｔ-φ_0ｊ）｝は翼経線上に分布する全てのダイポールにつき同位相となる。したがって位相干渉の無いことが知られる。

図６　スキュー翼の分布ダイポール

図６にスキュー翼の分布ダイポールを示す。　スキュー翼の場合も翼上を線素に分けて微小線素ごとにダイポールを分布させ音圧を算出する。ただしダイポールは, 普通翼での推力分布(普通翼で求まった推力の強さ分布)を翼スパン方向に保持したまま所定のスキュー曲線（翼弦の前縁から1／4の所を結んだ曲線）に取られた線素上に分布させる。発生音圧の式は式(4)と同じ形であるが，ダイポール音源中心位置番号j(j＝1,2,．．，J)における初期位相角φ_0jがスキュー曲線上で全て異なるので位相差が発生する。すなわち位相干渉により発生音圧が普通翼に比べ小さくなることが想定される。

以上，普通翼及びスキュー翼の発生音圧算出法を構築した。

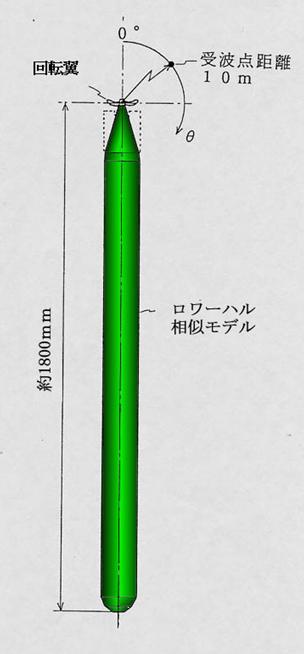
図７　ロワーハル相似モデル

構築した普通翼とスキュー翼の発生音圧算出式を用い発生音圧を数値計算で求め比較を行った。計算においては，ロワーハルに回転翼が付くのでロワーハルによる音波反射の影響も考慮に入れる。回転翼が発生する音波（直接波と呼ぶ）と直接波がロワーハルに作用し新たに発生する音波（反射波と呼ぶ）の二つを考え、図７に示すようなロワーハル相似モデル周りの音場を計算する。ただしロワーハルを剛（ロワーハルが振動せずロワーハル内部に音波透過しない）とする。また反射音場は文献^１１）による手法を採用した。

表1に回転翼運用条件を示す。

3．1　　普通翼とスキュー翼の指向性について比較検討

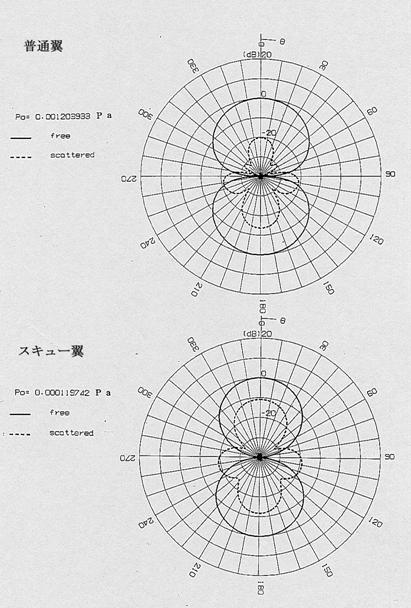
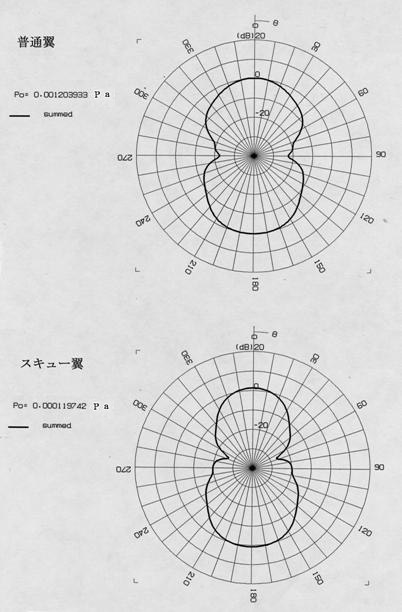
先ず，ロワーハル相似モデル端部に付けた回転翼中心周り10ｍでの発生音圧の方向特性(指向性)を求め比較する。図８−１に11.2ｋＨｚの場合の普通翼とスキュー翼の直接波及び反射波の指向性を示す。実線(freeと表示)は直接波の指向性パターン，破線(ｓｃａｔｔｅｒｅｄと表示)は反射波の指向性パターンである。図８−２に普通翼とスキュー翼の直接波と反射波を位相を考慮して加算した合成音圧(summedと表示)を示す。ロワーハル相似モデルの前方が180度方向と一致する。図中普通翼,スキュー翼のＰ_０はそれぞれの0度方向の直接波の音圧(単位Ｐａ表示)であり，指向性パターンは全てこのＰ_０の値で規格化した。理由は，スキュー翼の場合普通翼に比べて音圧レベルが低くパターンが小さく表示されるためである。

図8−１　11.2ｋＨｚの普通翼とスキュー翼の指向性計算値(直接波、及び反射波)

図８−２　11.2ｋＨｚの普通翼とスキュー翼の指向性計算値(合成波)

普通翼もスキュー翼も直接波，反射波，合成波の全てにおいて，０degと１８０degの方向に指向性が付いている。これより回転翼の発生音が送受波器の装備される１８０ｄｅgの方向に大きく出ることが判る。しかし直接波のP₀の値は普通翼で１．２０３９×１０^−３Pa，スキュー翼で１，１９７×１０^−４Ｐａとなり，スキュー翼の発生音圧は普通翼に比べて20ｄＢ低い。0ｄｅｇ以外の方位についても普通翼よりスキュー翼の発生音圧が小さく，スキュー翼では全方位について２０ｄB以上発生音圧の低減効果があることが判る。

図９−１に25.2ｋＨｚの場合の普通翼とスキュー翼の直接波及び反射波の指向性を示す。図９−２に25.2ｋＨｚの普通翼とスキュー翼の合成波の指向性を示す。

図9−1　25.2ｋＨｚの場合の普通翼とスキュー翼の指向性計算値(直接波、及び反射波)

図9−2　25.2ｋＨｚの普通翼とスキュー翼の指向性計算値(合成波)

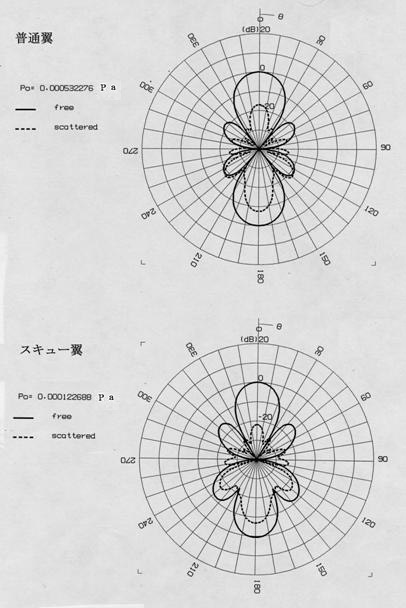
２５．２ｋＨｚでは，直接波，反射波及び合成波のいづれも0degと180ｄｅｇに指向性が付いている。ただし周波数が11.2ｋＨｚより高い今の場合，直接波において図のようにサイドローブが45deg，135degに現れる。さらに反射波は180ｄｅｇに指向性が強くなり合成波において分るように180deｇの音圧レベルが普通翼でもスキュー翼でも上がっている。直接波のP₀の値は普通翼で５．３２３×１０^−４Pa，スキュー翼で１，２２７×１０^−４Ｐａである。スキュー翼の発生音圧は普通翼に比べて１２．７ｄＢ低い。また0ｄｅｇ以外の方位についても普通翼よりスキュー翼の発生音圧が小さく，スキュー翼では全方位について１２ｄB以上発生音圧の低減効果があることが判る。

これまでの結果から，スキュー翼では翼スパン方向に分布するダイポールの位相干渉により，全方位に対し発生音圧が低減されることが判った。次に周波数領域で普通翼とスキュー翼の発生音圧を比較する。

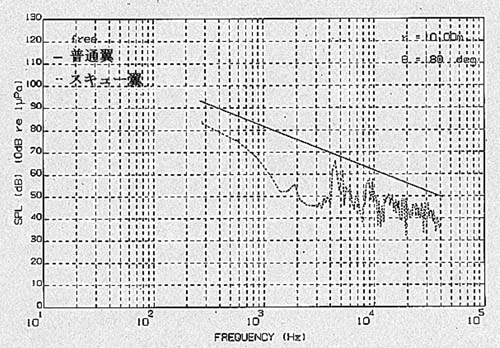
3．2　　普通翼とスキュー翼の周波数に対する発生音圧について比較検討

ここでは，送受波器の付くロワーハル相似モデル前方180degの受波音圧を計算し，普通翼とスキュー翼の直接波の発生音圧を比較を行った。図1０に普通翼とスキュー翼について直接波の受波音圧周波数特性を示す。図から判るように全ての周波数においてスキュー翼の音圧が下回っている。スキュー翼では，翼スパン上のダイポール音源の位相干渉により発生音が相殺されるためと考えられる。周波数によってダイポールの位相干渉の相違があるため一定したレベルで低減されないが，４．５ｋHzと９ｋHz付近を除けば10dB以上の音圧低減効果がある。

図10　普通翼とスキュー翼の直接波の受波音圧周波数特性

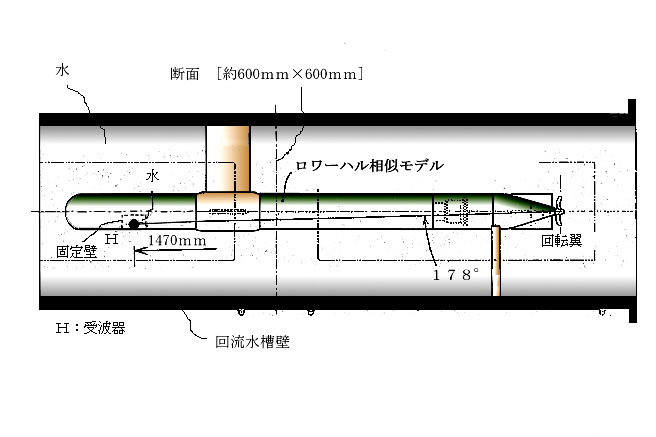
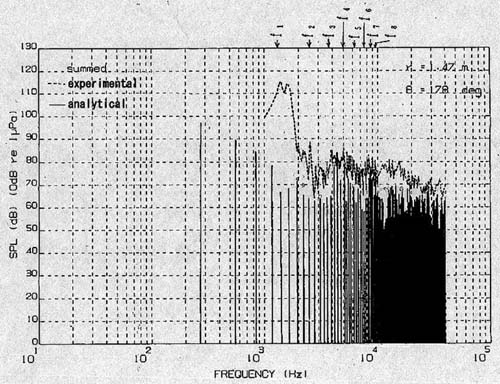
４．　実際のロワーハル相似モデルの発生音圧実験値と計算値の比較

　本計算手法検証のためロワーハル相似モデルを製作しその発生音圧と計算値の比較を行った。実験に用いたロワーハル相似モデルの形状寸法は図７と同じである。回転翼は図６と同じものを用いた。回転翼の運用条件を表2に示す。図１１に実験の説明図を示す。ロワーハル相似モデルを，図のような回流水槽(断面寸法は約600mm×600mm)内で中心軸が水槽壁と平行となるように固定した。水は流速6.25m／sで左側から右側に移動する。更に受波器を図のHで示される箇所に取り付けた。受波器は回転翼中心を原点とした極座標（ｒ，θ）＝（1470ｍｍ,178ｄｅｇ）で示す位置にありアルミ製殻の内部に固定壁で固定されている。また固定壁で覆われた内室は水が満たされている。又ロワーハルの後部にモータがあり回転翼と連結されている。

受波器では回転翼の発生音以外にとモータによる振動の発生音などが受波される。ここでは回転翼音のみを対象とするので，回転翼有りの受波音圧（モータと回転翼作動の受波音圧）から回転翼無しの受波音圧（モータのみ作動の受波音圧）を差し引いたものを回転翼の発生音圧とし，これを実験値とした。　そして計算値との比較を行った。

　図１２に，受波器の受波音圧周波数特性{実験値と計算値（直接波と反射波の合成音圧）}を示す。図より，1ｋHz〜3kＨzの範囲で実験値は計算値よりかなり高いことが知られる。これは，定在波の影響である。尚，定在波の共振位置を1次共振から8次共振まで同図にf₁，f₂，．．．，ｆ_８で示した。回流水槽断面が600mm×600mmと小さく，内壁を剛とすれば断面内に1.25kHzから定在波が立つ。

図12　受波器の受波音圧周波数特性{実験値と計算値（直接波と反射波の合成音圧）}

１０ｋHz以上の高周波域においては，実験値と計算値の差が小さいことが判る。この辺りになると高周波の特性から定在波の減衰が大きく，差が小さくなると推定される。又ロワーハルの振動による固体音が実験で発生しておりその差がこの高周波域に残るものと思われる。今回実験設備の関係上（使用した回流水槽は，本来流体力学的な諸特性の試験をするために設計されており壁などには吸音材が無い），どうしても定在波の影響は取り除けなかったが，計算値はオーダ的に比較的実験値と合っていると思われる。

５．まとめ

海洋調査双胴船のロワーハルに付く回転翼のノイズ低減について，回転翼をスキュー翼にした場合の発生音を求め普通翼の発生音と比較検討した。また計算で用いたロワーハルモデルと同じモデルを製作し，実際に回流水槽内で回転翼が発生する音圧を計測し，構築した発生音圧算出法の計算値と比較した。検討結果，

１）      ここで用いたスキュー形状翼では，普通翼に比べ発生音圧が１０ｄＢ以上低減されることが判った。スキュー翼形状にすることで極めて高い騒音低減効果が得られる。

２）      実験において回転翼が発生する音圧と計測値とは，回流水槽内に発生する定在波の影響を除けばほぼ同じようなオーダーとなることが判った。

構築した回転翼の発生音圧式は妥当性があるものと思われる。

今回，ロワーハルの振動を考慮しなかったが，モータ起振力によりロワーハル外殻が振動し固体音として伝わる音圧が大きいと想定される。何故ならば，金属製のロワーハルの外側に存在する水は，音響インピーダンスが金属と近いオーダーであるため固体音が水へと伝搬されるためである。今後そのあたりを考慮できるように改善していくつもりである。

参考文献

１）M.V.Lowson；"Theoretical Analysis of Compressor　Noise,”J.Acoust.Soc.Am.47(1)(part2),371-385,（1970）

２）守屋：[空気力学序論]，(培風館，東京，昭和50年)，p148〜p156

３）M.J.Lighthill:”On Sound Generated aerodynamically.　I　.　General　Theory　,”Proc.　Roy　.Soc.(London),211a,1107,p564-587,(1952)

４）森口，他２名；「数学公式�V−特殊関数」，第�W篇　Ｂｅｓｓｅｌ函数，ｐ１４５〜 （岩波，東京，1977年）

５）C.Morfey and H.K.Tanna;”SOUND RADIATION FROM A POINT FORCE IN CIRCULAR MOTION”,J.Sound Vib.15(3),p325〜p351,(1971)

６)Harvey H.Hubbard;”Aeroacoustics of Large Wind Turbines”,J.Acoust.Soc of Am.89(6),(1991),p2495〜p2508

７）「プロペラ翼の発生音場に関するダイポール音源近似の一考察」未発表

８）犬井；「偏微分方程式とその応用」，（コロナ社，東京，昭和50年），ｐ234〜ｐ240

９）文献４；§４０　球Ｂｅｓｓｅｌ函数，ｐ１４５〜， 第�X篇　球函数　第２章　Ｌｅｇｅｎｄｒｅ陪函数　，ｐ１２０〜（岩波，東京，1977年）

１０) William K.Blake,”mechanics of Flow-induced Sound and Vibration”,Complex Flow-Structure Interactions,Vol.�U，ｐ843〜ｐ847，(ACADEMIC　PRESS，INC．1986)

１１）トピックス１５；[有限長弾性円筒による散乱音場の検討]，‘０４．４．１