作図法(2)
 証明(2.1)
 証明(2.2)
 解説(2)

メニューのページへ
 トップへ

（作図法(2)）
　辺OBの中点をDとする。直線OCに平行な直線と直線OAとの交点をEとする。直線DE上に
　　　(28)
を満たすように点Fをとる。ただし、AとFは直線OCに関し反対側にあるものとする。直線CDと直線OAとの交点をGとし、直線FG と直線OCとの交点をHとする。
　直線OA上に
　　　(29)
を満たすように点Iをとる。ただし、AとIはOに関し同じ側にあるものとする。３点A,H,Iを通る円と直線OHとの交点をJとする。 JからOAに下ろした垂線と線分HJの垂直二等分線との交点をKとする。Kを中心としHを通る円と直線OAとの交点をPとすると、 直線CPが三角形OABの面積をニ等分する。
　ただし、作図の過程でPが存在しない場合は、点Cを通りかつ線分OA,OBの両方と交わる直線で三角形OABの面積が二等分されることはない。
　Pに相当するものが２個ある場合は、そのそれぞれをPとし、上の作図を２回試みるものとする。
　線分OAが円Kと交わらないまたは線分OBが直線PHと交わらない場合は、そのPからは条件を満たす直線が得られない。
　同様の作図を頂点O,A,Bを読み替えて３回繰り返せば、三角形OABの面積を二等分する直線でCを通るものがすべて得られる。
（証明(2.1)）
　（作図により得られる直線が三角形OABの面積を二等分すること。）
　直線CPと直線OBとの交点をQ、直線HPと直線OFとの交点をRとする。Kを中心としHを通る円と直線OAとの交点のうち、Pでない方を P'とする。
　方べきの定理より、
　　　(30)
である。(29)より、
　　　(31)
である。
　　　(32)
と円周角の定理、対頂角の相等より、
　　　(33)
である。さらに、
　　　(34)
であるから、三角形OP'Hと三角形ORHは合同である。ゆえに、
　　　(35)
(31)(35)より、
　　　(36)
３点P,Q,Rは同一直線上にあるから、メネラウスの定理より、
　　　　　
　　　(37)
３点P,C,Qは同一直線上にあるから、メネラウスの定理より、
　　　　　
　　　(38)
HCとFDが平行であるから、
　　　(39)
(37)(38)(39)より、
　　　　　
　　　　　
　　　(40)
(36)(40)より、
　　　　　
　　　　　
　　　　　
したがって、直線PQは三角形OABの面積を二等分する。
(証明(2.2))
　（（証明(2.1)）の逆、すなわち、点Cを通る直線で線分OA、OBの両方に交わるものが作図により得られること。）
　点Cを通る直線が、線分OA、OBの両方に交わるとし、その交点をP,Qとする。さらに、
　　　(41)
が成り立っているものとする。点D,E,F,H,I,J,Kは作図方のところで述べたようにとる。直線PHと直線OF、OBとの交点を R',Q'とすると、（証明（2.1））の(36)から(40)まではQをQ'、RをR'と読み替えれば成り立つから、
　　　(42)
(41)(42)より、
　　　(43)
ここで、半直線OA上に
　　　(44)
を満たすように点P"をとれば、
　　　(45)
(29)(45)より、
　　　(46)
これと方べきの定理（A,I,H,Jは同一円周上にある）より、
　　　(47)
であるから、4点P,P",H,Jは同一円周上にある。この円の中心をK'とすると、Kは線分HJの垂直二等分線上にある。また、 (44)より、三角形OP"Hと三角形OR"Hは合同である。これと、円周角の定理、対頂角の相当から、
　　　(48)
(48)より、
　　　(49)
したがって、K'はJからOAに下ろした垂線の上にある。
　ゆえに、K'は作図により得られるKと一致するから、この直線PQは作図により得られるものの一方と一致する。
　この作図法のアイデアは、次のような一次変換の性質を知っていると分かりやすくなります。ただし、一次変換は現行の 教育過程では、高校で学ばなくなってしまっています。一次変換の性質についてまったく知識がないかたは、適当な参考書 をご覧下さい。
　ある直線上にある２つの線分を一次変換でうつしたとき、長さの比はその前後で保たれる。
　２つの三角形を一次変換でうつしたとき、面積の比はその前後で保たれる。
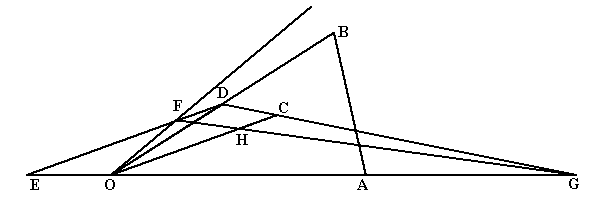
このことの証明は他にゆずるとして、これにより作図のアイデアがわかります。以下のようにすると、 ”平面上の任意の点Cを通る直線で三角形の面積を二等分する問題”を”三角形の一つの角の二等分線上にある 任意の点Hで三角形の面積を二等分する問題”に言いかえることができ、作図がだいぶわかりやすくなります。
　いまOを原点とするとき、Aを不動点にもち、かつ、直線OCを不動直線にもち、かつ、直線OBを直線OFにうつすような 一次変換が存在する。この一次変換を f とすると、
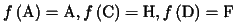　　　(48)
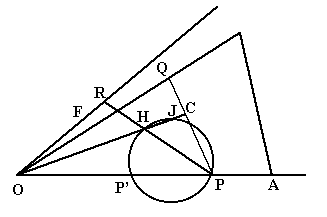
Hを通る直線を l' とし、これと直線OA、OFとの交点をP,Rとする。三角形OPRと三角形OAFの面積が等しいように l' が定まれば、直線 f -1(l' ) がCを通り、三角形OABの面積を二等分する直線 l となる。方べきの定理より、
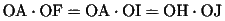　　　(48)
であるから、
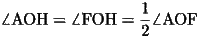　　　(48)
とすると、三角形OAFの面積は、
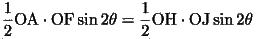　　　(48)
となる、三角形OAFと三角形OPRの面積が等しいとすると、
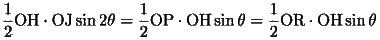　　　(48)
より、
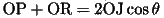　　　(48)
となる。ここで、半直線OA上にOR=OP'を満たすように点P'をとれば、
　　　(48)
が成り立つ。Jから直線OA上に下ろした垂線の足をLとすると、三角比の定義により、
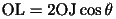　　　(48)
であるから、
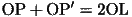　　　(48)
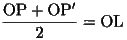　　　(48)
ゆえに、Lは線分PP'の中点である。さらに、
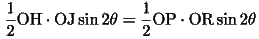　　　(48)
より、
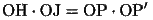　　　(48)
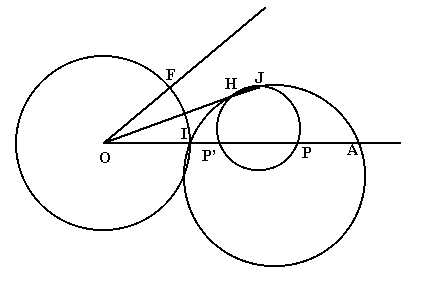
ゆえに、４点H,J,P,P'は同一円周上にある。この円の中心をKとすると、直線JLが線分PP'の垂直二等分線であるから、Kは 直線JL上にある。すなわち、Kは直線JLと線分HJの垂直二等分線の交点である。これでK,Pの作図法がわかった。こうして 得られる直線HPを l' として l=f -1(l' ) をもとめればよいのだが、Pは不動点であるから、 l は直線CPに一致する。
メニューのページへ
 トップへ