\begin{split} １ &: \ コマの減衰（ 空気抵抗・軸受の摩擦抵抗） \\ ２ &: \ 二重コマの才差運動\\ ３ &: \ 二重コマの章差運動\\ ４ &: \ 二重コマの才差運動の加速\\ ５ &: \ フレームの回転の加速・減速\\ ６ &: \ フレームの接地面の摩擦力\\ ７ &: \ フレームの接地面の摩擦力により生じるモーメント力\\ & \hspace{ 70pt } （フレームは起き上がろうとする）\\ \end{split}

　少なくとも以上の力・モーメント力が相互作用しながら回転する為、地球コマは回すたびにその挙動が変わります。章差運動がハッキリと判る動画は撮れなかったのですが、才差運動が加速しているのは判ると思います。

　私が持っている地球コマを数度回しただけで『中心角一定で才差運動するコマなど、世の中に存在しない。』と断定するのは乱暴な気がします。ですが、次の　才差運動の理論解　を読んで頂ければ納得してもらえるかもしれません。

02　才差運動の理論解

　まず、教科書に書いてある説明です。

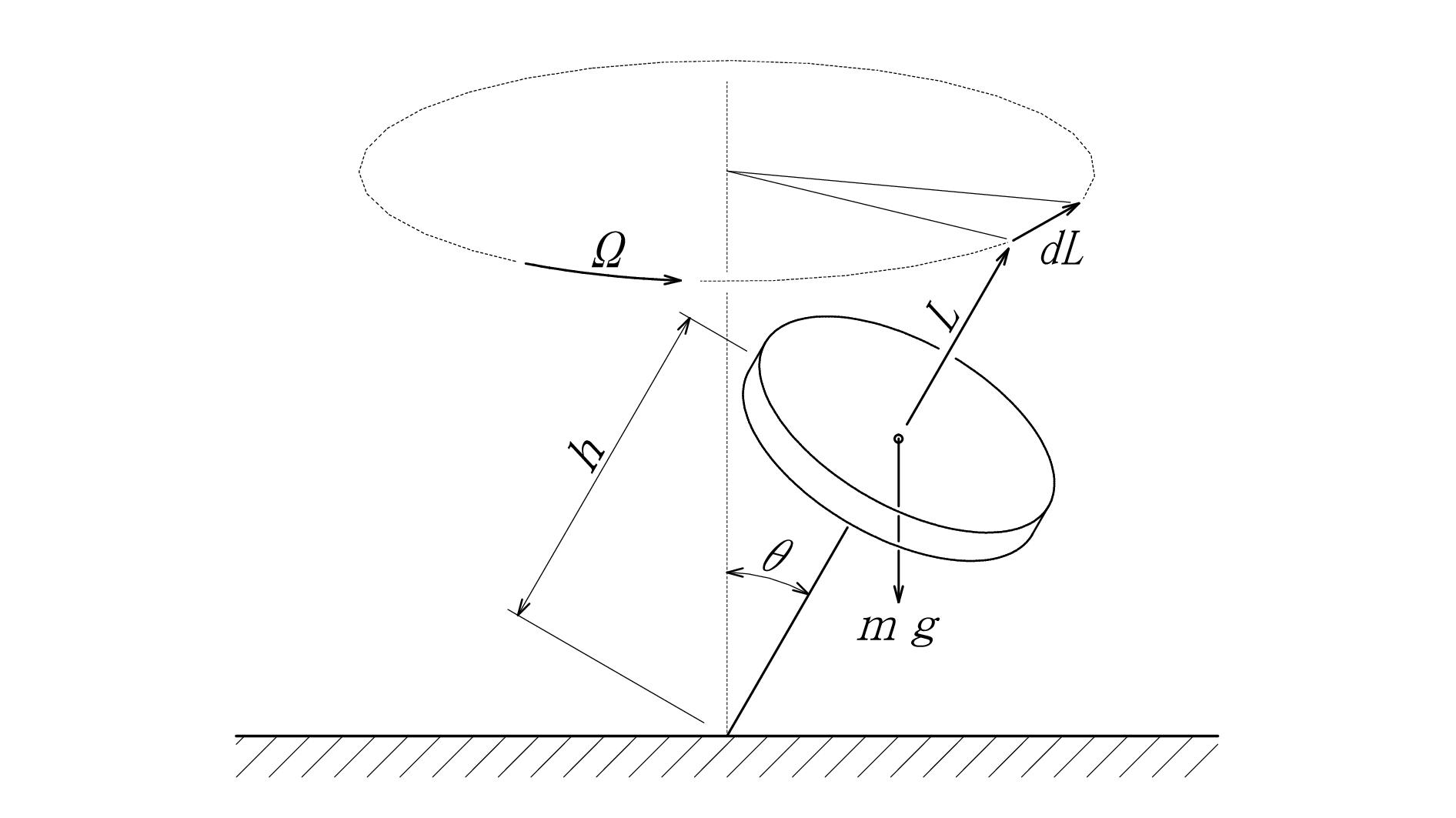
図 - 01

\[ dL = mgh \sin θ \]

　『才差運動により生じた角運動量変化 \(dL\) と重力のモーメント \(mgh \sin θ \) が釣り合う。』　と書いてあります。この説明は、コマが倒れないことの説明にはなっています。

\[ 才差運動している = コマが動いている \]

のですから、静力学的なモーメント力の釣合で説明できる訳がありません。少なくとも空気抵抗に逆らって才差運動しているわけですから下の図に示す \(\color{red}{dL_z}\) が存在し、それに釣合うモーメント力が存在しないことを示さなければ、才差運動の説明にはなりません。

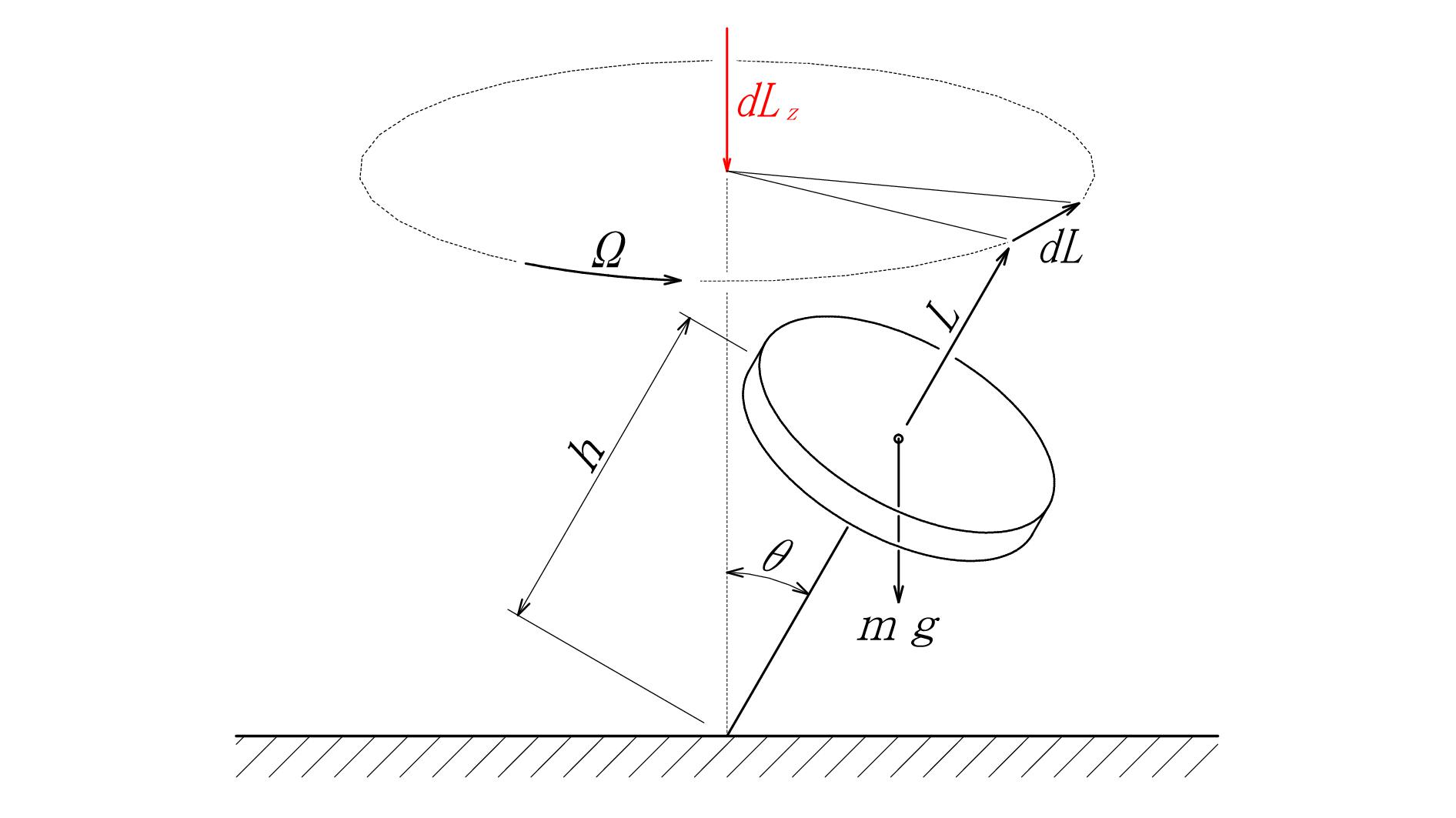
図 - 02

　まず最初に私が気が付いたのは”才差運動による遠心力”です。

　図 - 01 に才差運動による遠心力項を加えます。

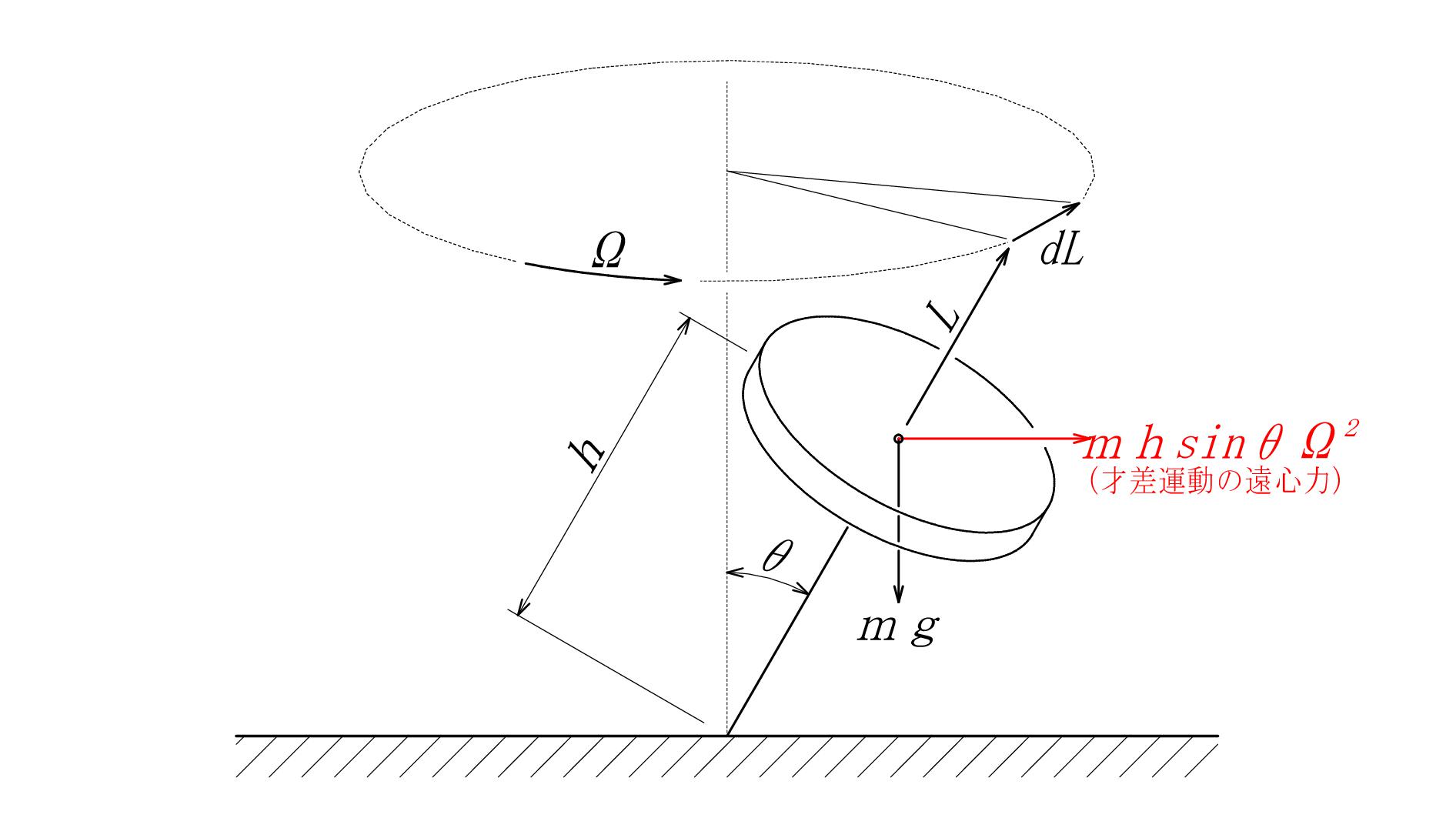
図 - 03

　これだけでは解くことが出来ません。これを解くためには、上の図の中に、あと二つ要素を見つけなければなりません。

　図 - 03 の重力 \( mg \) と才差運動の遠心力 \(mh \sin θ\ Ω^2 \) をモーメント力の表示 \( dL_g \)， \( dL_s \) に切り替え、 \( dL \) を \( dL_l \) と表示します。

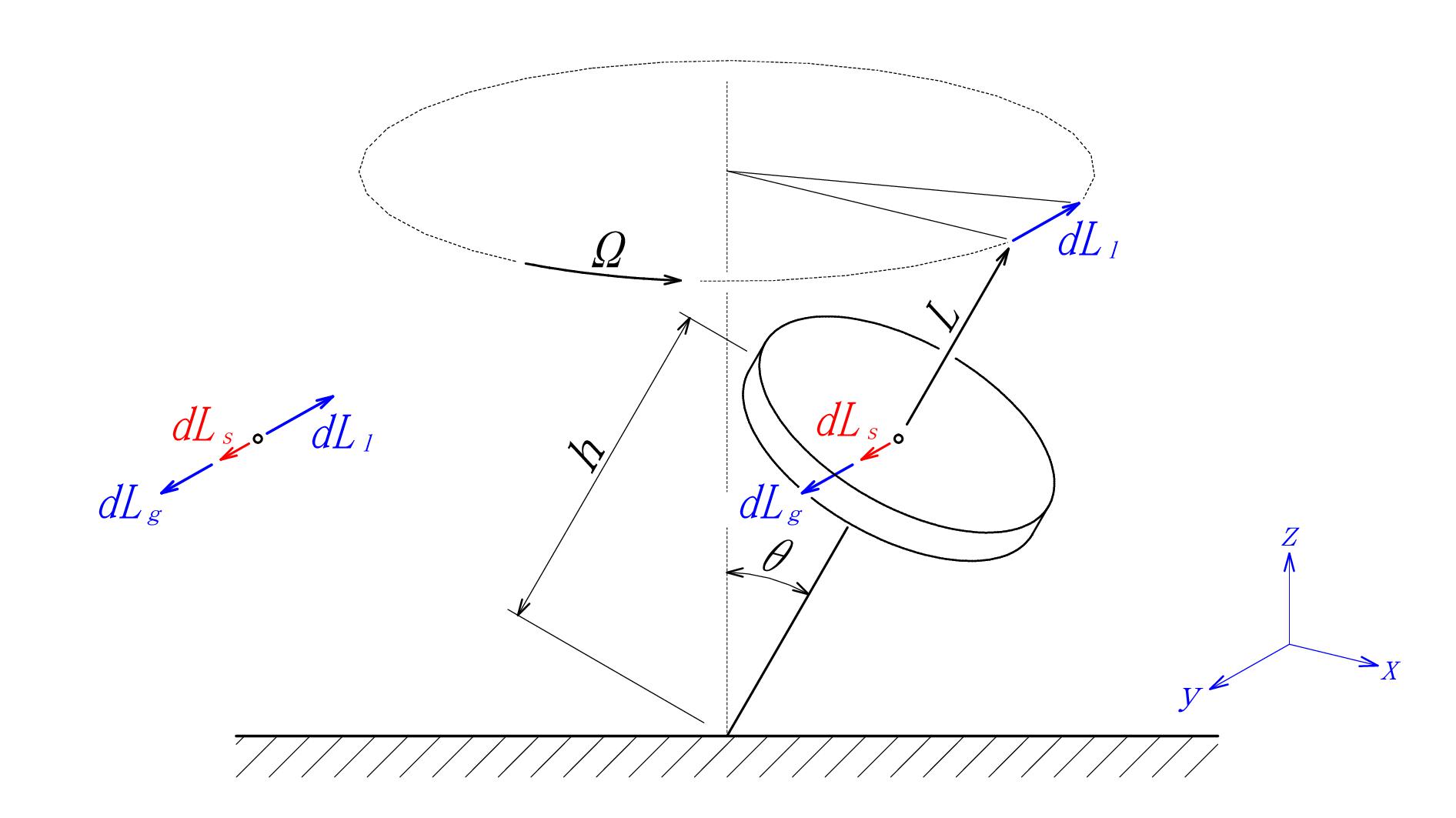
図 - 04

\begin{split} \color{blue}{dl_g} &\ :\ 重力によるモーメント力\\ \color{red}{dl_s} &\ :\ 才差運動の遠心力によるモーメント力\\ &\hspace{ 140pt }とした場合\\ \end{split}

\begin{eqnarray} \color{blue}{dl_g}\ &=& \ \color{blue}{mgh \sin θ} \\ \color{red}{dl_s}\ &=& \ \color{red}{h \cos θ\ mh \sin θ\ Ω^2} \\ \end{eqnarray}

　一般的には　\( \color{blue}{dl_g} + \color{red}{dl_s} ≠ \color{blue}{dL_l} \)　となり章差運動が発生します。

　\( \color{blue}{dl_g} + \color{red}{dl_s} \gt \color{blue}{dL_l} \)　の場合には、中心角は徐々に大きくなりコマは倒れていきます。

　\( \color{blue}{dl_g} + \color{red}{dl_s} \lt \color{blue}{dL_l} \)　の場合には、中心角は徐々に小さくなり最終的にコマは直立します。

　\( \color{blue}{dl_g} + \color{red}{dl_s} = \color{blue}{dL_l} \)　の場合は、そんな場合はまず存在しないのですが、コマは教科書に書いてある通り中心角一定で才差運動します。

　図 - 03 の中で見つけなければならない二つの要素の内、一つ目の要素はコマの章差運動です。地球コマが回転している動画の数秒～十数秒を切出せば、地球コマは中心角一定で回転しているように見えるのですが、実際にはかなりゆっくりとですが、立上り又は倒れこみの運動をしています。

　ここでは、コマが倒れこんでいるとして図の中に一つ目の要素を加えます。

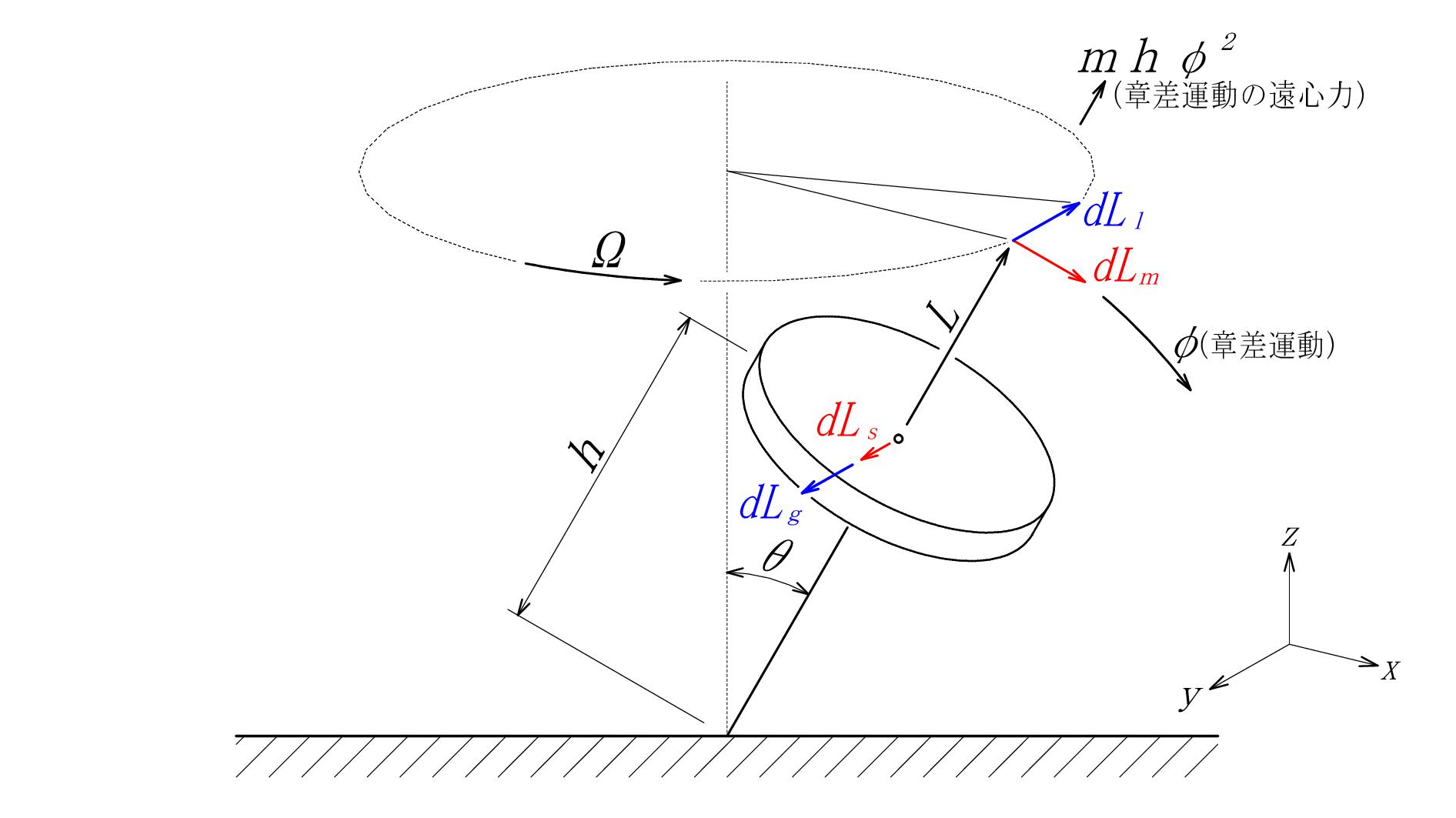
図 - 05

　とりあえず、章差運動による角運動変化 \( \color{red}{dL_m} \) を加えました。上の図により四次方程式が立てられるのですが、この方程式を解くことは出来ませんでした。

　方程式を諦めて、\( \color{blue}{dL_l} \) と \( \color{red}{dL_m} \) の角度関係に注目することにしました。 \( \color{blue}{dL_l} \) と \( \color{red}{dL_m} \)が直交していることに気が付くと、自動的に二つ目の要素があることに気が付きます。

　 \( \color{blue}{dL_l} \) と \( \color{red}{dL_m} \)に直行する成分 \( \color{red}{ dL_n } \) 、コマの減衰成分です。

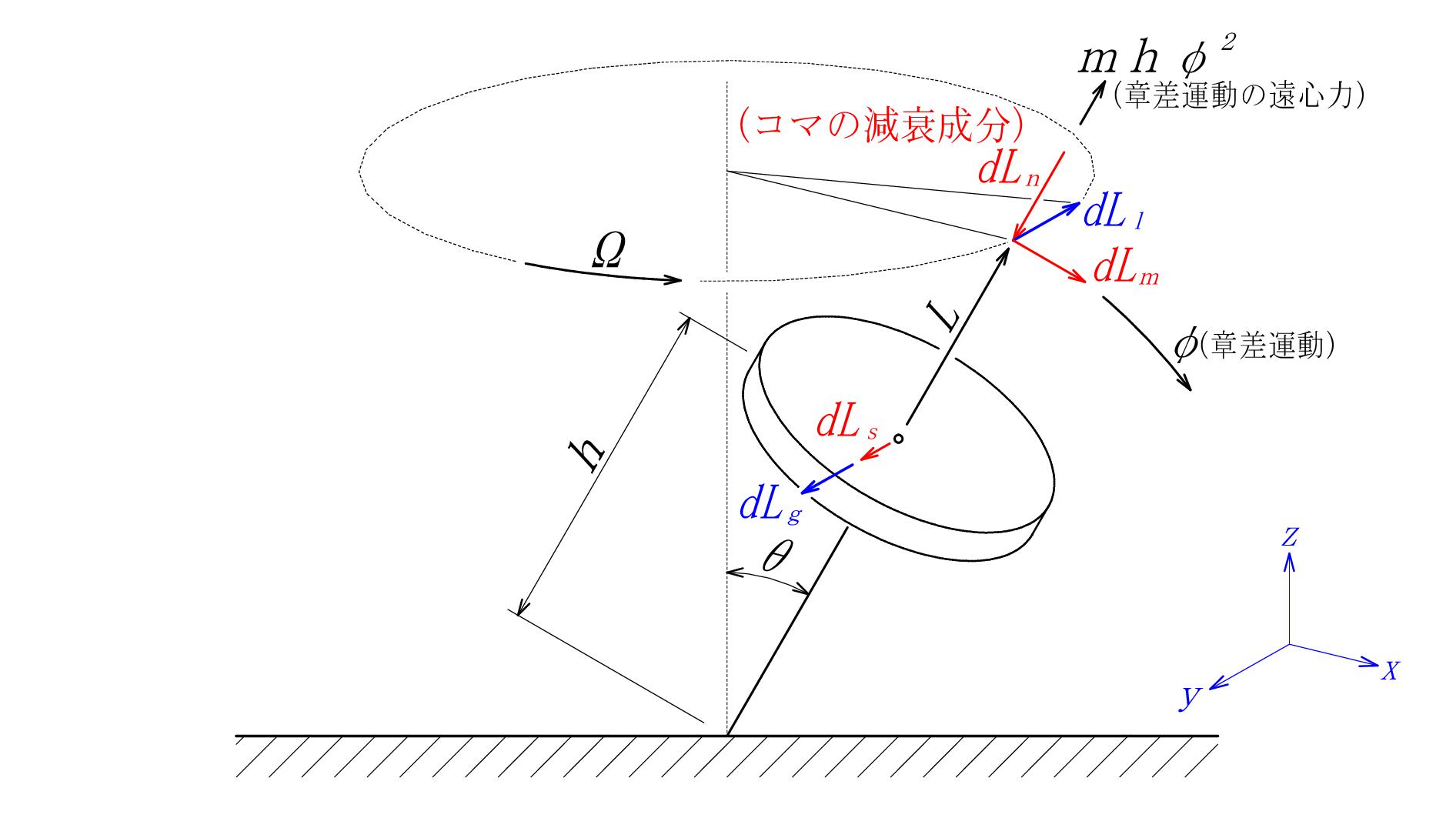
図 - 06

　 \( \color{red}{ dL_n } \) コマの減衰成分です。これで解けました。

\[ ( \ \color{blue}{dL_l} \ , \color{red}{dL_m} \ , \color{red}{dL_n} \ ) = ( \ dL_x \ , dL_y \ , dL_z \ ) \tag{02-01}\ \]

　 \( \normalsize{ lmn } \) 系から見た角運動量の変化が、 \( \normalsize{ xyz } \) 系から見た角運動量の変化に等しい。

　 ここで

\begin{split} \color{blue}{dL_l} &: \ コマの才差運動により発生するモーメント力 \\ \color{red}{dL_m} &: \ コマの章差運動により発生するモーメント力\\ \color{red}{dL_n} &: \ コマの減衰成分\\ dL_x &: \ x 軸方向のモーメント力 \\ dL_y &: \ y 軸方向のモーメント力 \\ dL_z &: \ z 軸方向のモーメント力（才差運動を駆動するモーメント力） \\ \\ （\color{red}{dL_s} &: \ 才差運動の遠心力によるモーメント力） \\ （\color{blue}{dL_g} &: \ 重力によるモーメント力） \\ \end{split}

　では、\(x,y,z\)　の各方向のモーメント力について見ていきましょう。まず \(x\)方向です。 \(\color{blue}{dL_l}\) の方向が \(y\)軸の方向と一致した瞬間の \(x-z\) の平面を切り出すと

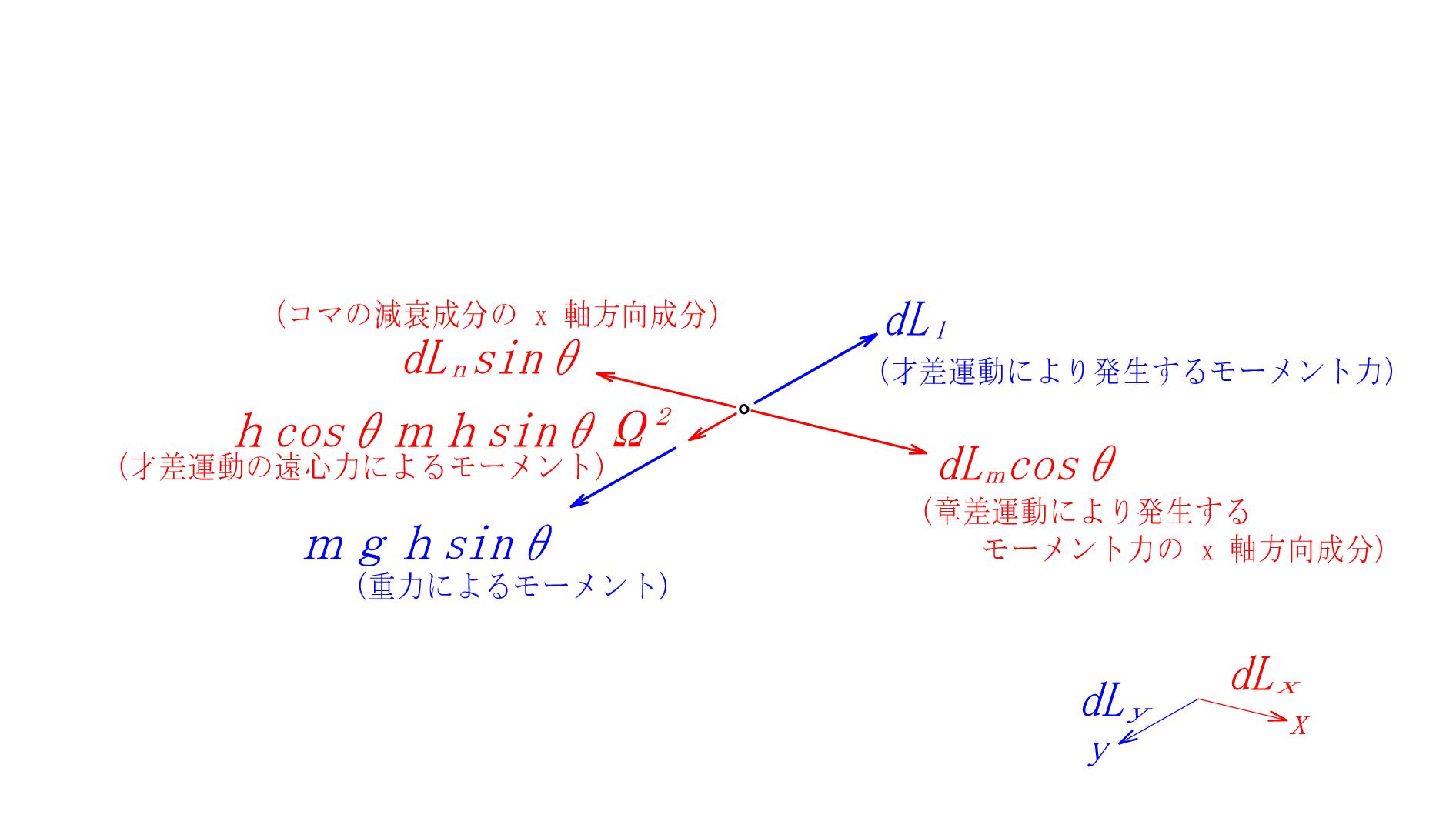
図 - 07

となります。

\[ \color{red}{ dL_x } = \color{red}{ dL_m \ \cos θ } \ - \ \color{red}{ dL_n \ \sin θ } \tag{02-02} \]

　\( \color{red}{dL_x} \) は通常ゼロにはなりませんが、この方向にコマの回転の自由度が無い( \( \normalsize{ y } \) 軸（章差運動） \( \normalsize{ z } \) 軸（才差運動）廻りに回転可能ですが、 \( \normalsize{ x } \) 軸廻りに回転不可能)ため、コマの系は不安定系となります。動いているのですから当然です。静力学的な力の釣合で説明できる訳が有りません。
　また、 \( \color{red}{dL_x}\) は、コマの接地点を押す（又は引く）力として作用している筈です。精密な秤の上でコマを才差運動させると、コマの質量変化として観測できるかもしれません。

　次が\( \normalsize{ y } \)方向です。 \(\color{blue}{dL_l}\) の方向が\( \normalsize{ y } \)軸の方向と一致した瞬間を考えると、図 – 6の左の図により

\begin{eqnarray} \color{blue}{ dL_y } &=& \color{blue}{ dL_l } \ - \ \color{red}{ dL_s } \ - \ \color{blue}{ dL_g \ } \\ &=& \color{blue}{\ dL_l} \ - \ \color{red}{ h \ \cos θ \ mh \ \sin θ \ Ω^2 } \ - \ \color{blue}{mgh \ \sin θ} \ \tag{02-03}\ \end{eqnarray}

　 \( \color{blue}{dL_y} \) が章差運動のモーメントです。一般的にこのベクトルもゼロにはならず、章差運動が起こります。 \( \color{blue}{dL_y}=0 \) とし、最終項（才差運動の遠心力項）を無視したのが、古典力学の才差運動の説明になります。

\begin{eqnarray} 0( \color{blue}{dL_y}) &=& \color{blue}{\ dL_l} \ - \ \color{red}{ 0 }（無視） \ - \ \color{blue}{mgh \ \sin θ} \\ \color{blue}{dL_l} &=& \color{blue}{mgh \sin θ} \hspace{ 70pt } 古典力学の説明 \end{eqnarray}

　\( y \)方向には、これらのモーメント力の他に　 フレームの接地面の摩擦力により生じるモーメント力（フレームは起き上がろうとする）が存在しますが、話が面倒になるだけなので、ここでは触れません。

　最後に\( z \)方向です。この方向のモーメント力が、才差運動の原因となります。\( x \)方向と同様に \( \color{blue}{dL_y} \) の方向が\( y \)軸の方向と一致した瞬間の\( x-z \)の平面を切り出すと

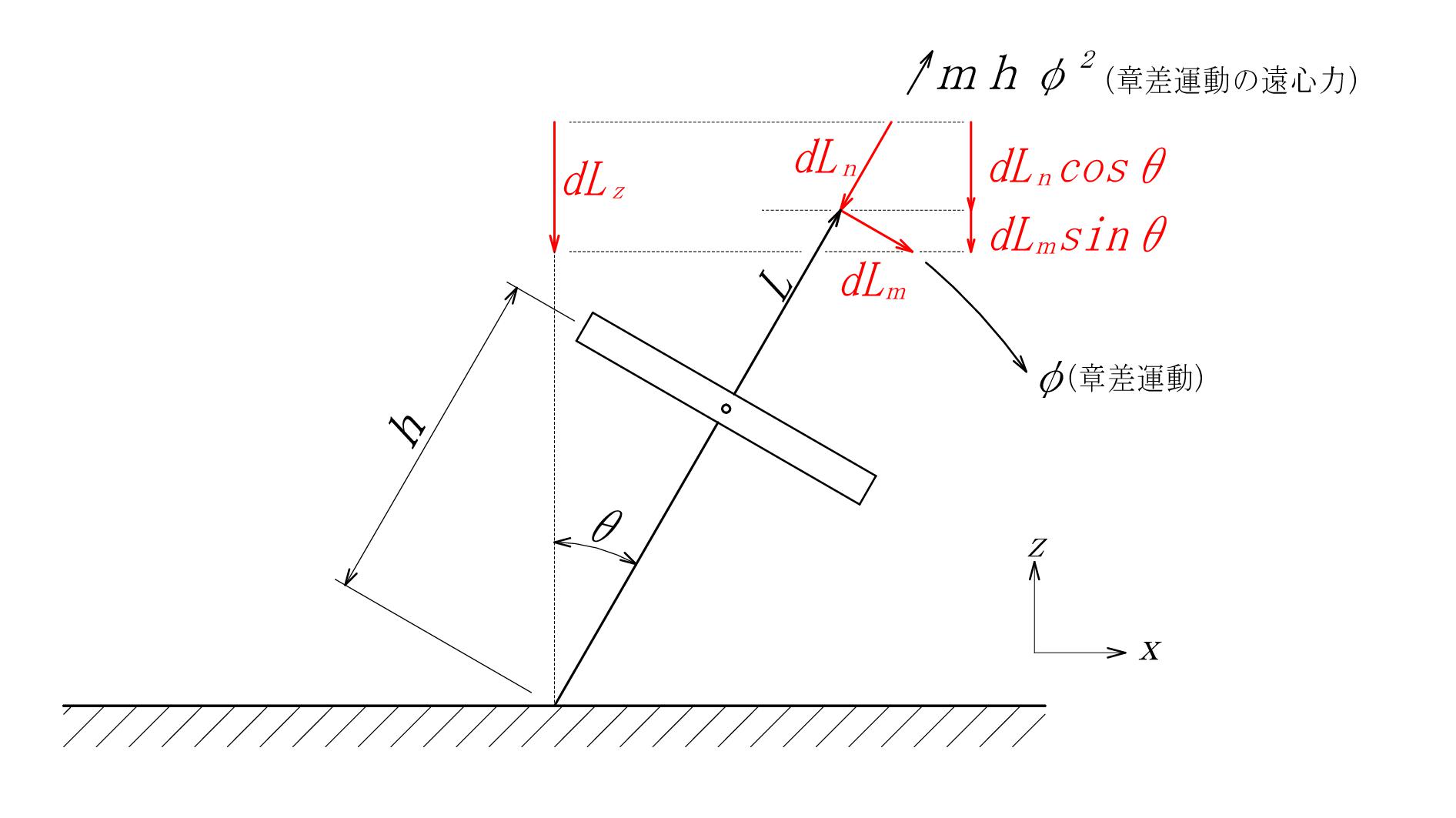
図 - 08

　図 - 08により

\[ \color{red}{ dL_z } = \color{red}{ dL_m \sin θ } + \color{red}{ dL_n \cos θ } \tag{02-04}\ \]

　\( \color{red}{dL_z}\) は才差運動 \( Ω \) の角加速度成分であり、これにより才差運動が引き起こされます。 \( \color{red}{dL_z} \) が空気抵抗と釣合うような特殊な場合を除き、一般的には才差運動は \( \color{red}{dL_z} \) により加速されます。

　 \( \color{red}{dL_z} \) の主な成分はコマの減衰成分です。モーターに取り付けられたコマのように、一定角速度で回転しているコマは、才差運動も章差運動もしません。ただし、電源を入れた直後や切った直後には、コマが加速・減衰するために、これらの運動が観察される場合が有ります。（糸で吊るしたモーター等）また、コマの回転軸が水平な場合も、コマの加速・減衰成分に \(ｚ \) 方向の成分が無い為に才差運動・章差運動は観察されません。

03　棒の法則

　2005年4月25日歯の痛みに耐えられず、朝一で歯医者に行きました。虫歯になった親知らずを速攻で抜かれ、11時頃部屋に戻りテレビをつけると、電車が脱線したニュースが流れていました。痛み止めを飲みボーとした頭で、ただボーとテレビを見ていました。

電車はなぜ脱線したのか？

尼崎の手前 300Rに入ったところで急制動をかけたらしい。

　電車一両あたりの重量は約 25ｔ。これが 300R を走行していました。つまり、重さ 25 t 直径 600m の巨大なコマが回転していたのと同じことになります。ゆえに、電車には巨大なコマとしての角運動量\(\ L_1\ \) が有ったことになります。

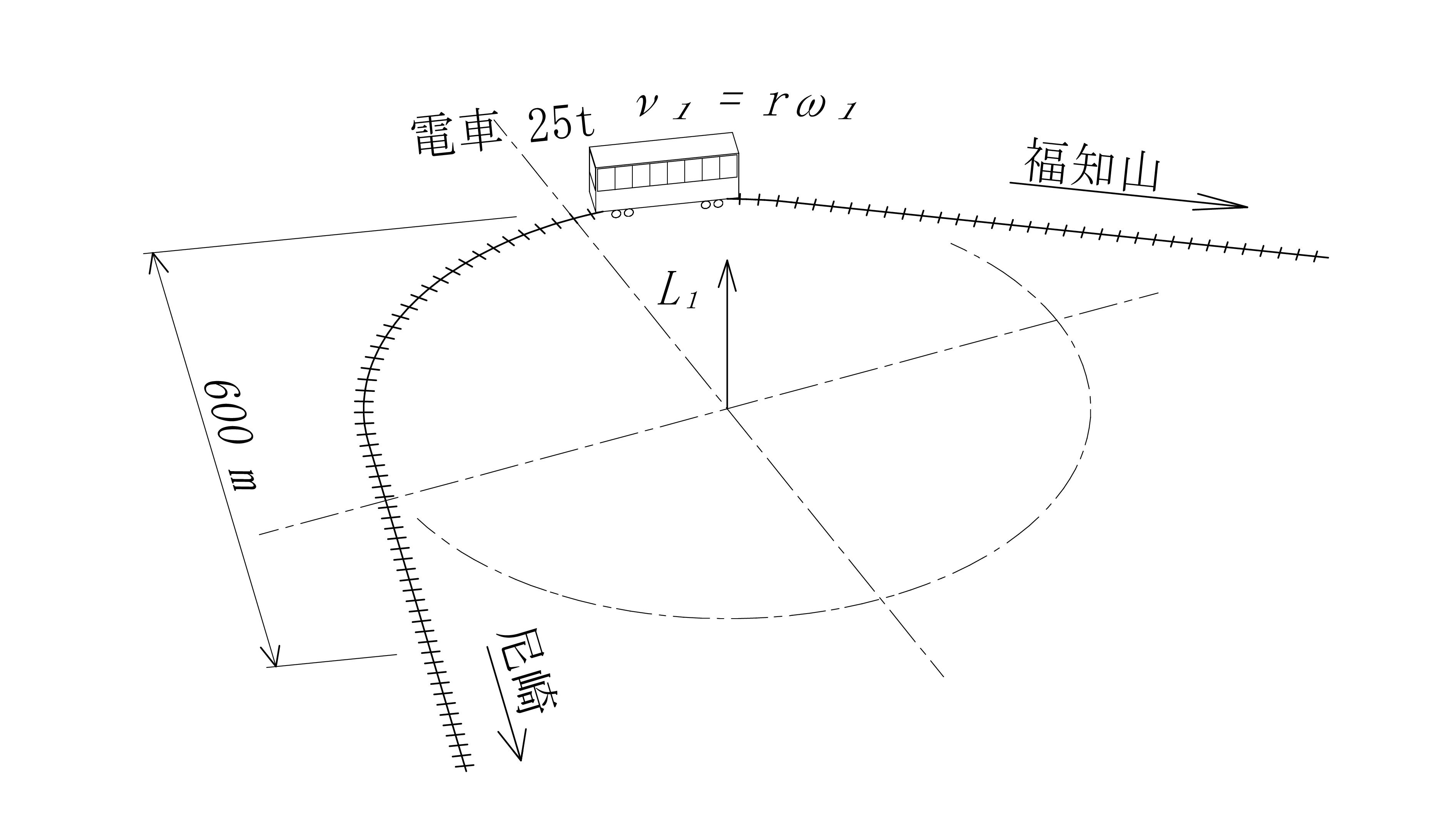
図 - 09

この巨大なコマに急制動をかけた事により、角運動量は\(\ L_1 → L_2\ \)となります。 その際、減衰モーメント\(\ \color{red}{dL}\ \)が発生します。

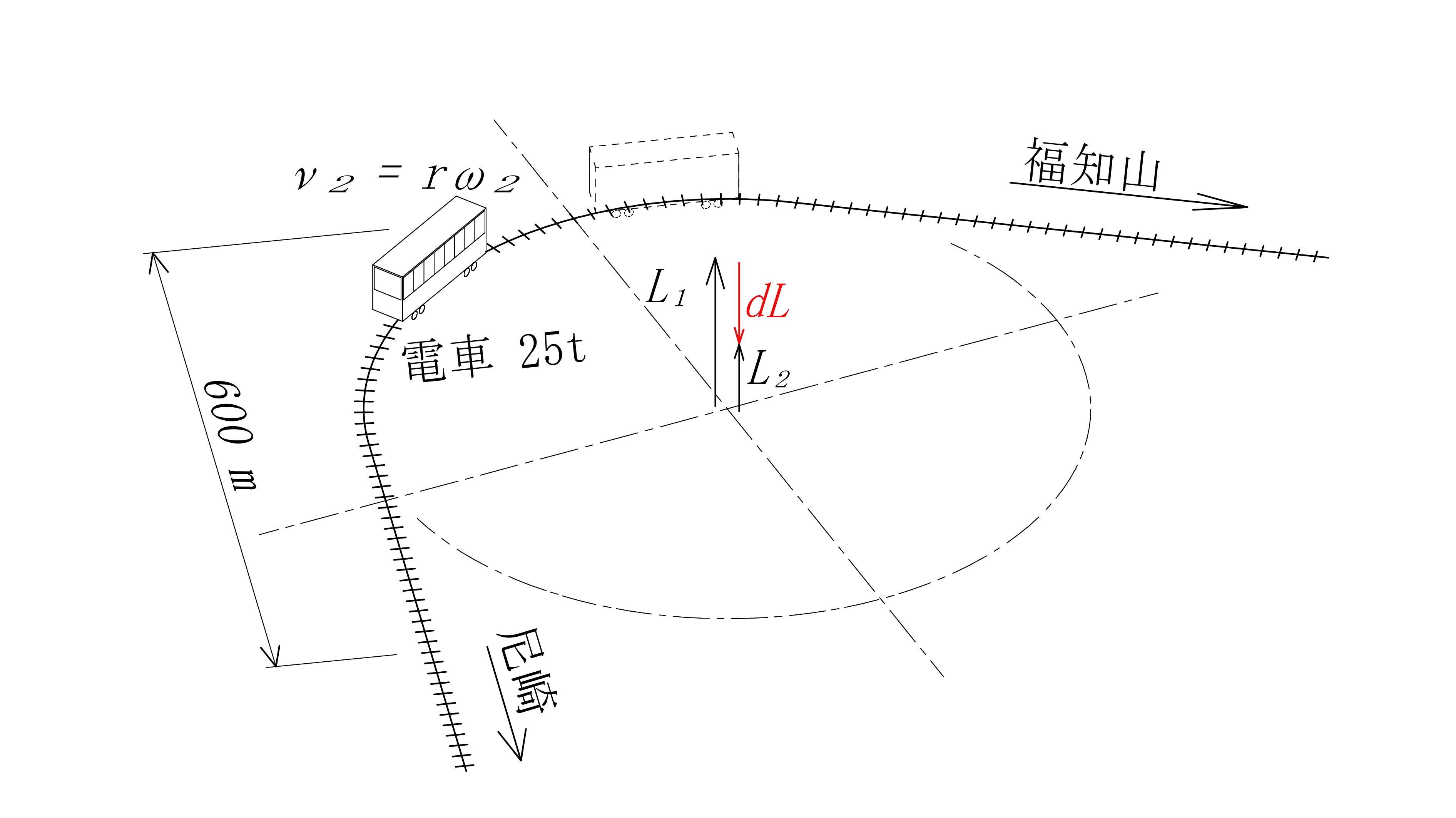
図 - 10

発生した減衰モーメント\(\ \color{red}{dL}\ \)は、電車の重心に作用します。

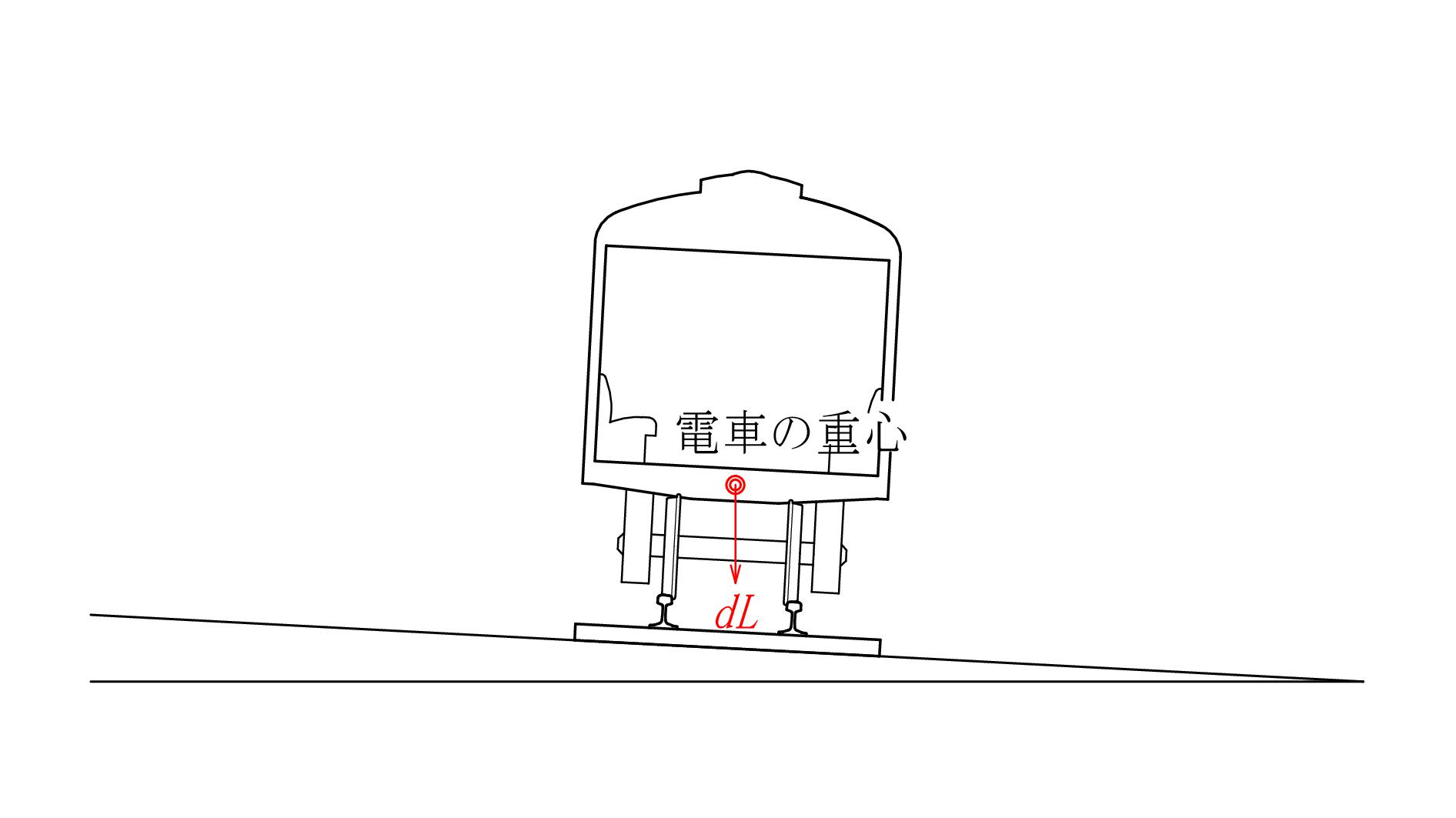
図 - 11

\(\ \color{red}{dL}\ \)は偶力として電車の車輪に作用し、前輪を軌道の外側に、後輪を軌道の内側に押す力として作用します。

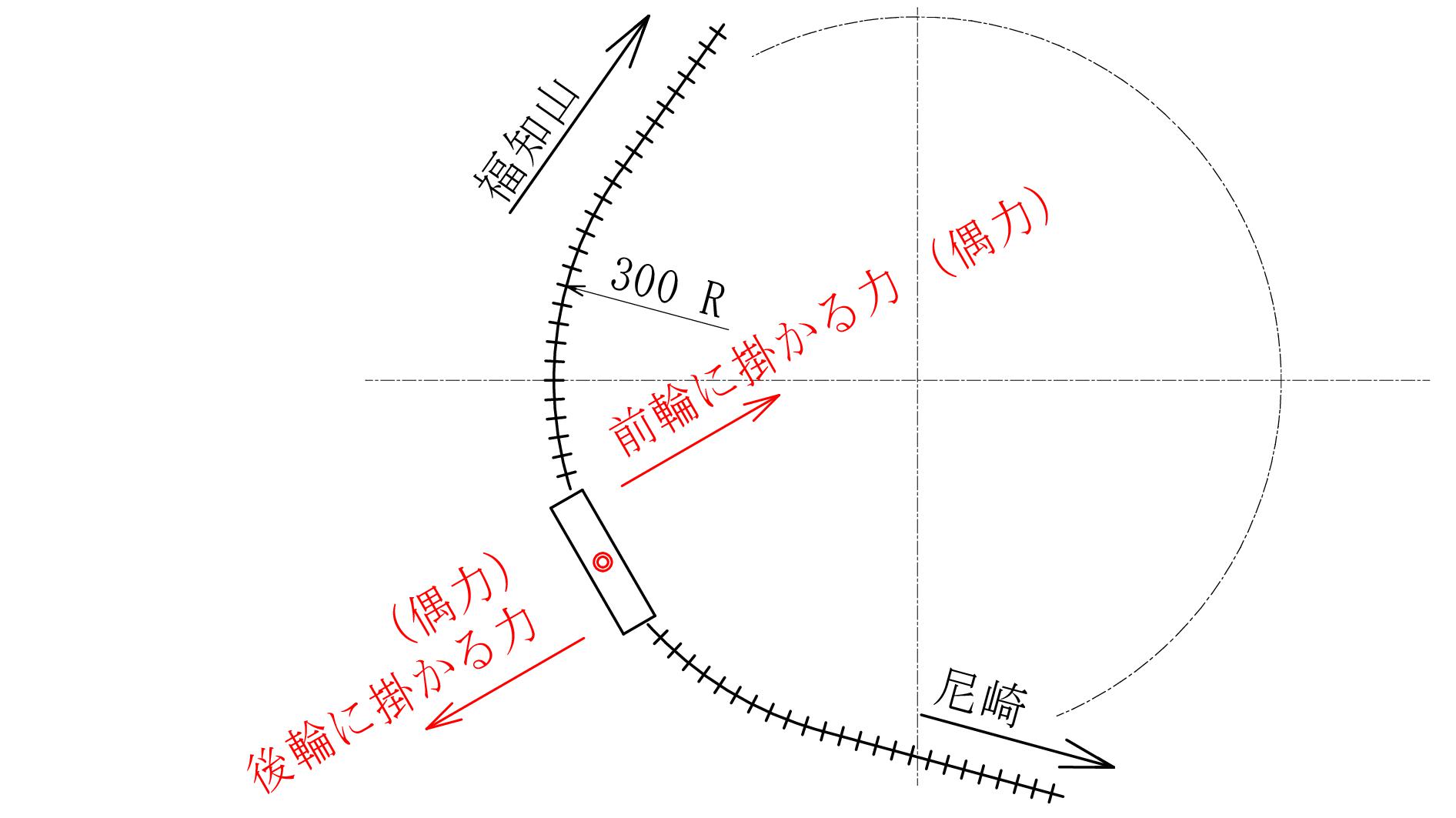
図 - 12

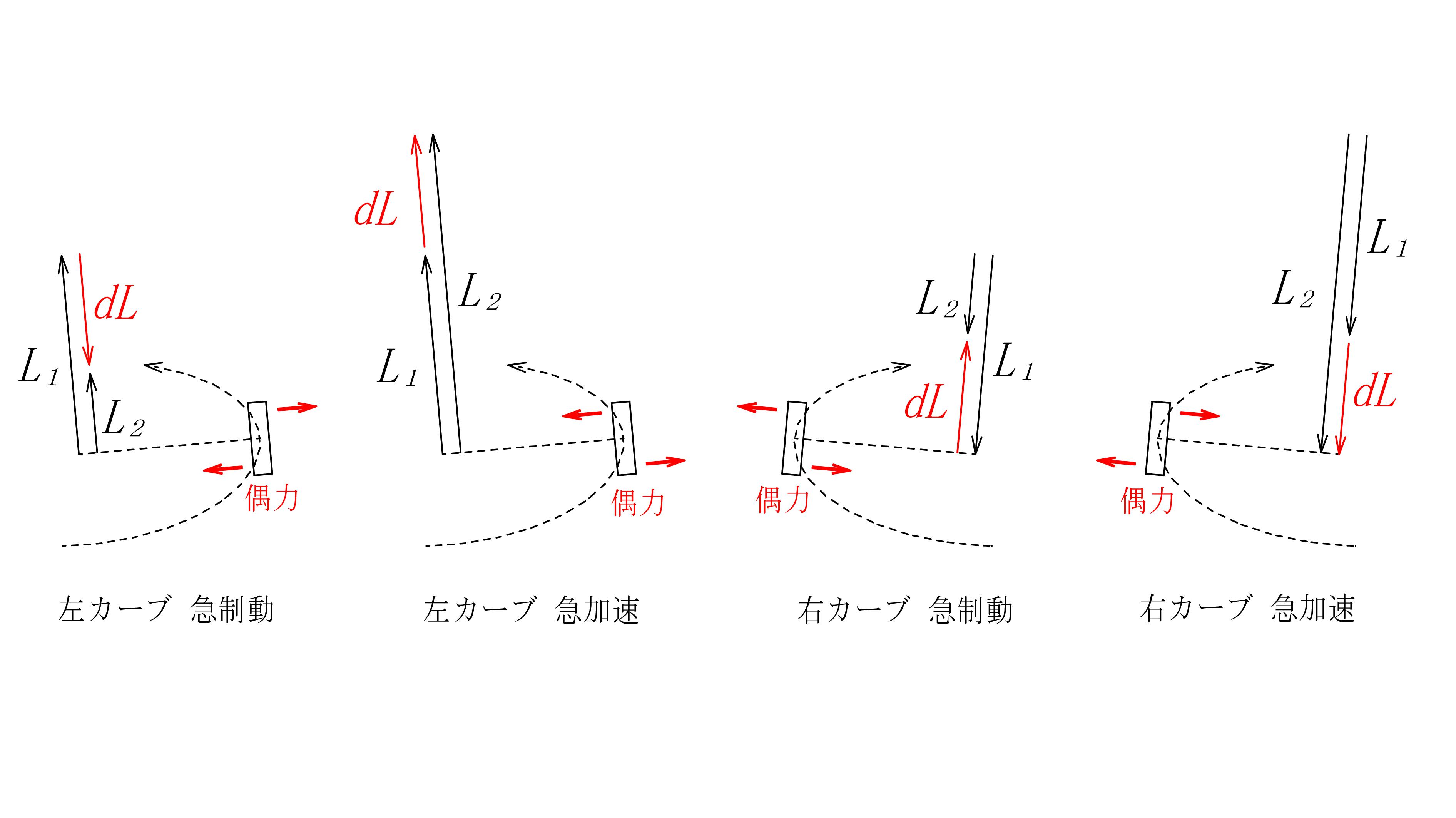
図 - 13

電車はなぜ脱線したのか？

遠心力・ドリフト以外に要因はないか？

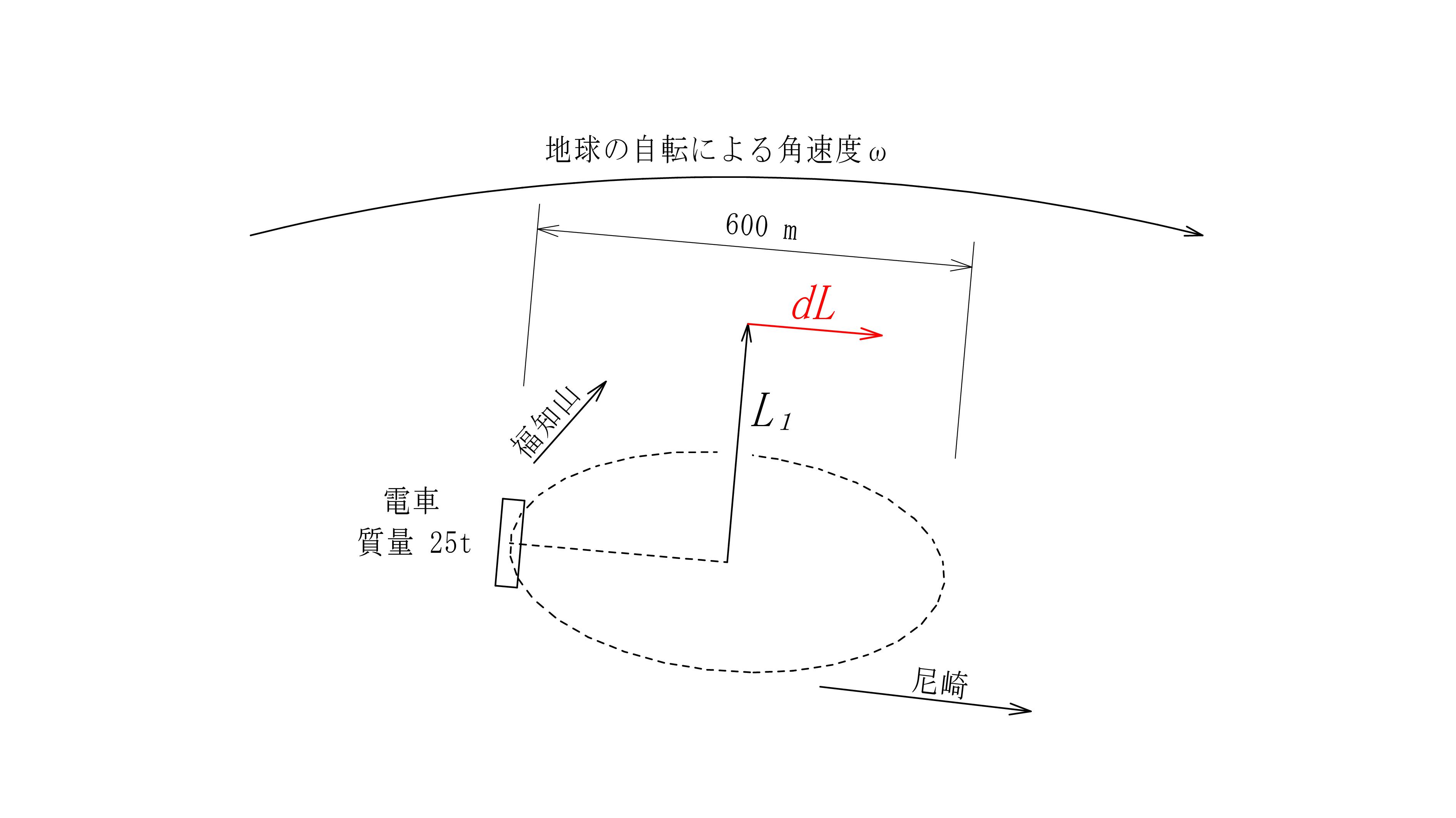
図 - 14

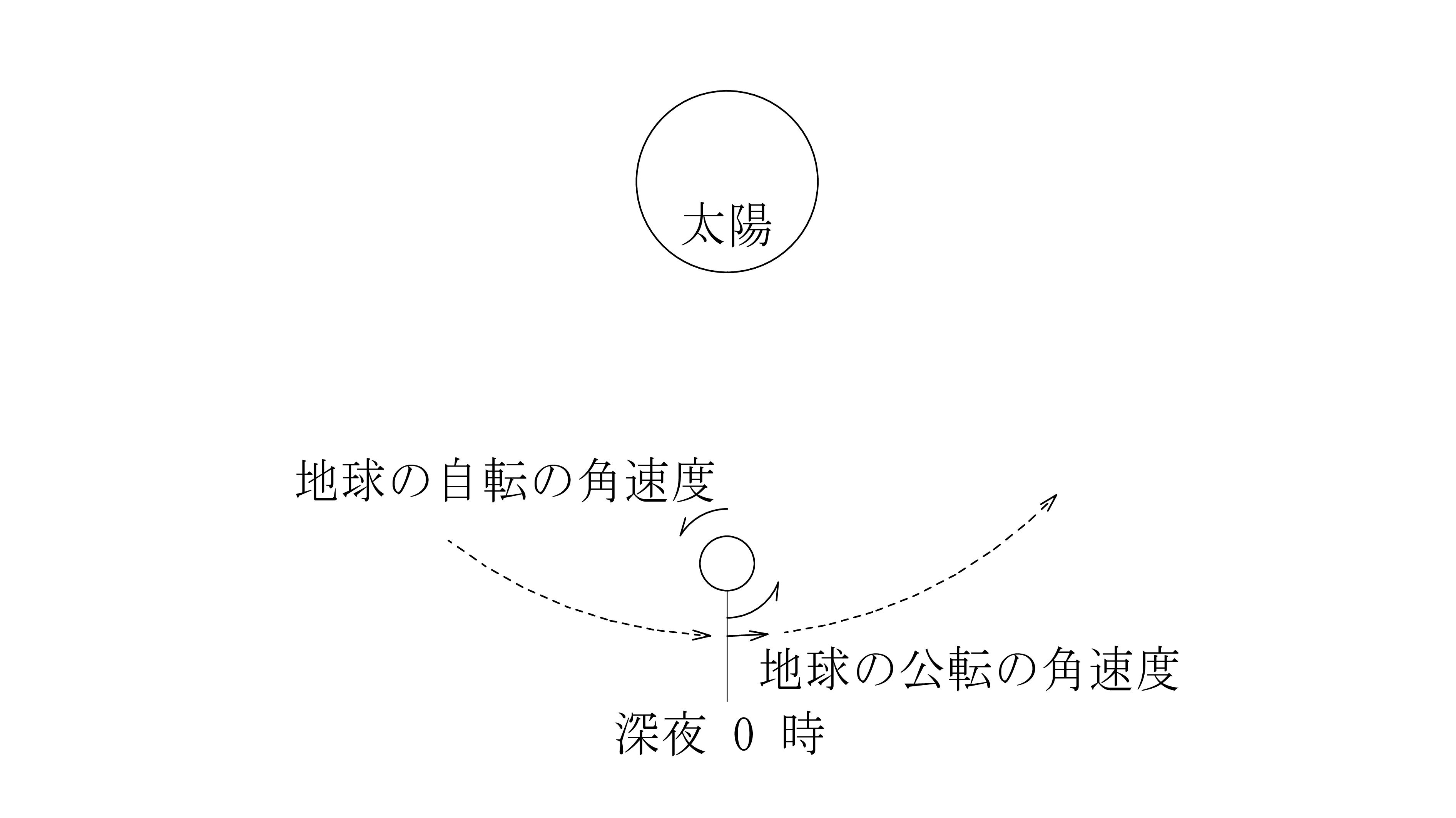
図 - 15

　太陽系は銀河系の縁に有り、銀河系は約2億5千万年の周期で自転しています。その銀河系は銀河団の中に有り、銀河団の周りを公転しています。（銀河団の自転）銀河団は超銀河団の中に有り・・・

地球　と　太陽

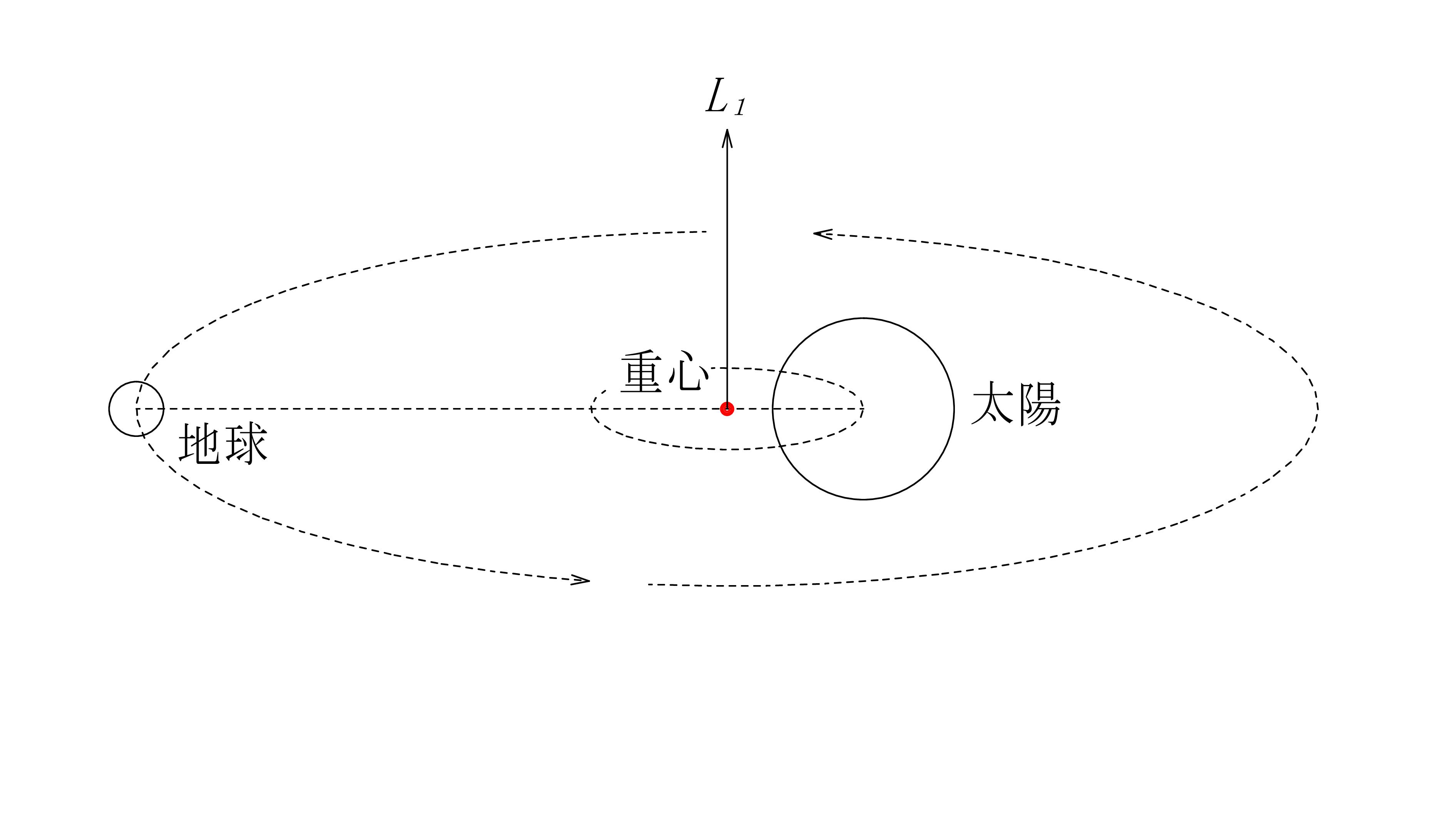
図 - 16

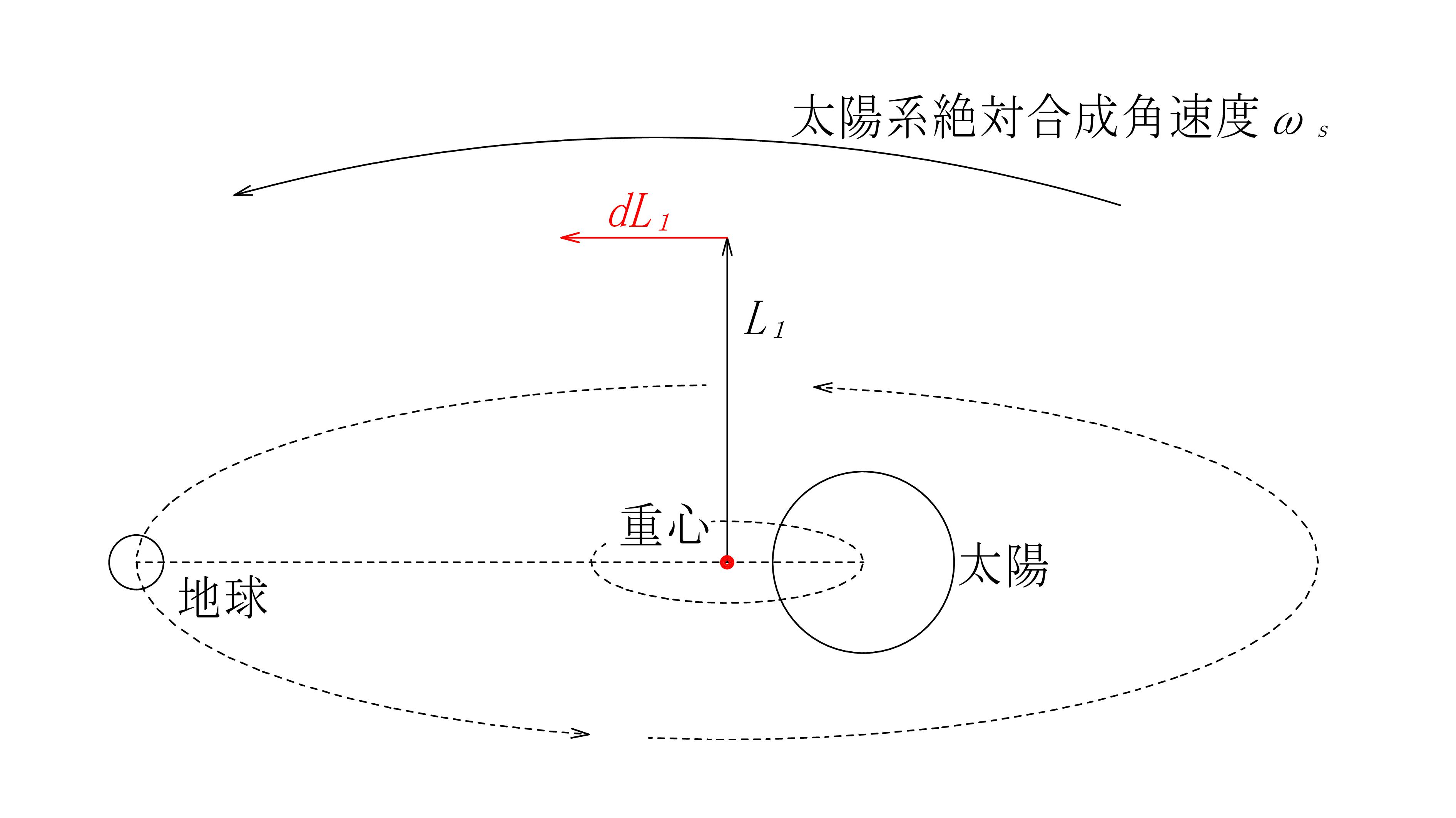
図 - 17

\begin{eqnarray} I_p &=& \sum mr^2\ \\ \\ &=& m_sr_s^2 + m_pr_p^2\quad（太陽項＋惑星項） \end{eqnarray}

\[ L_p = I_pω_p \]

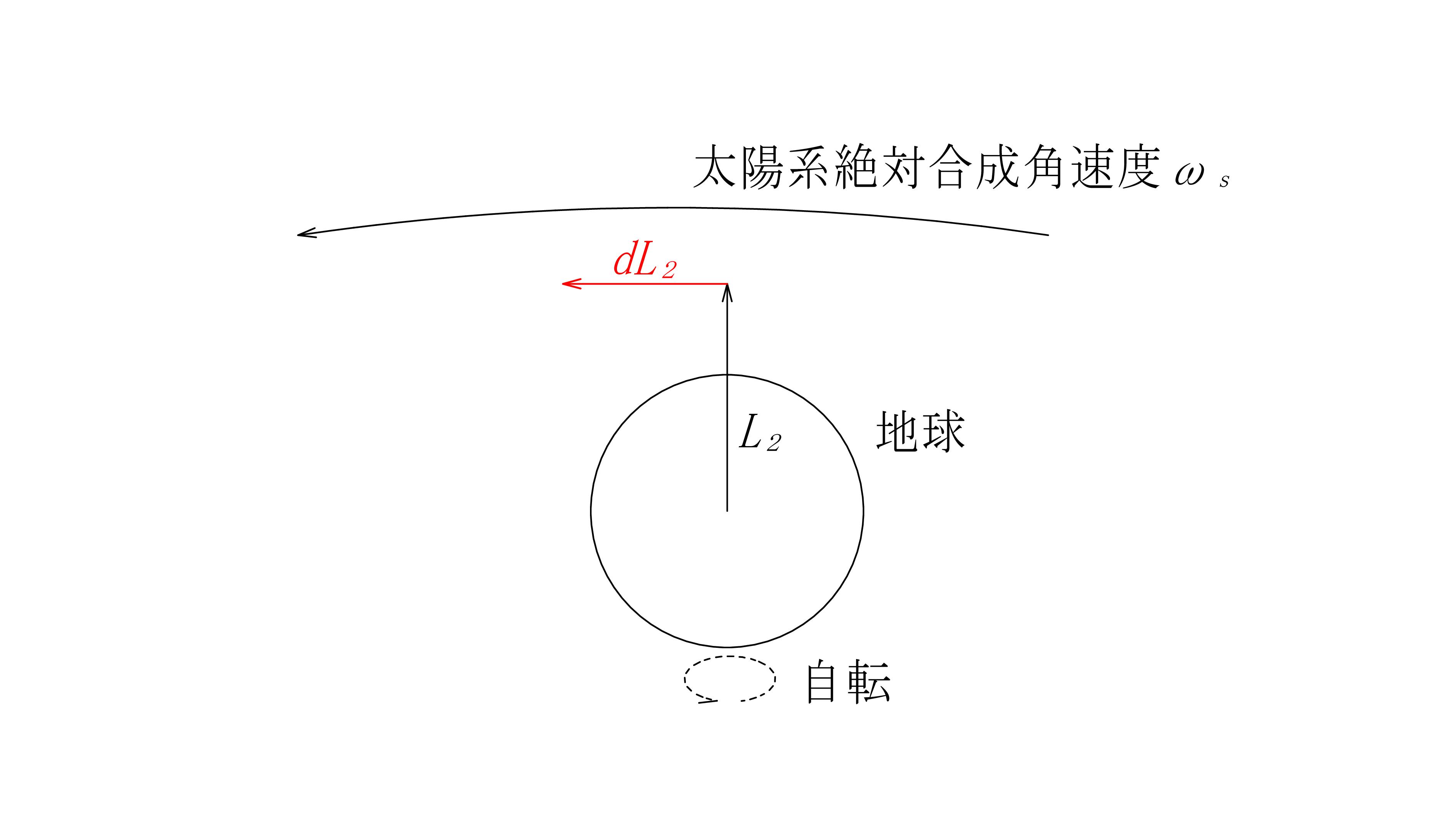
図 - 18

惑星の軌道面が傾く運動は、なぜ止まってしまったのか？

地軸が傾く運動は、なぜ止まってしまったのか？

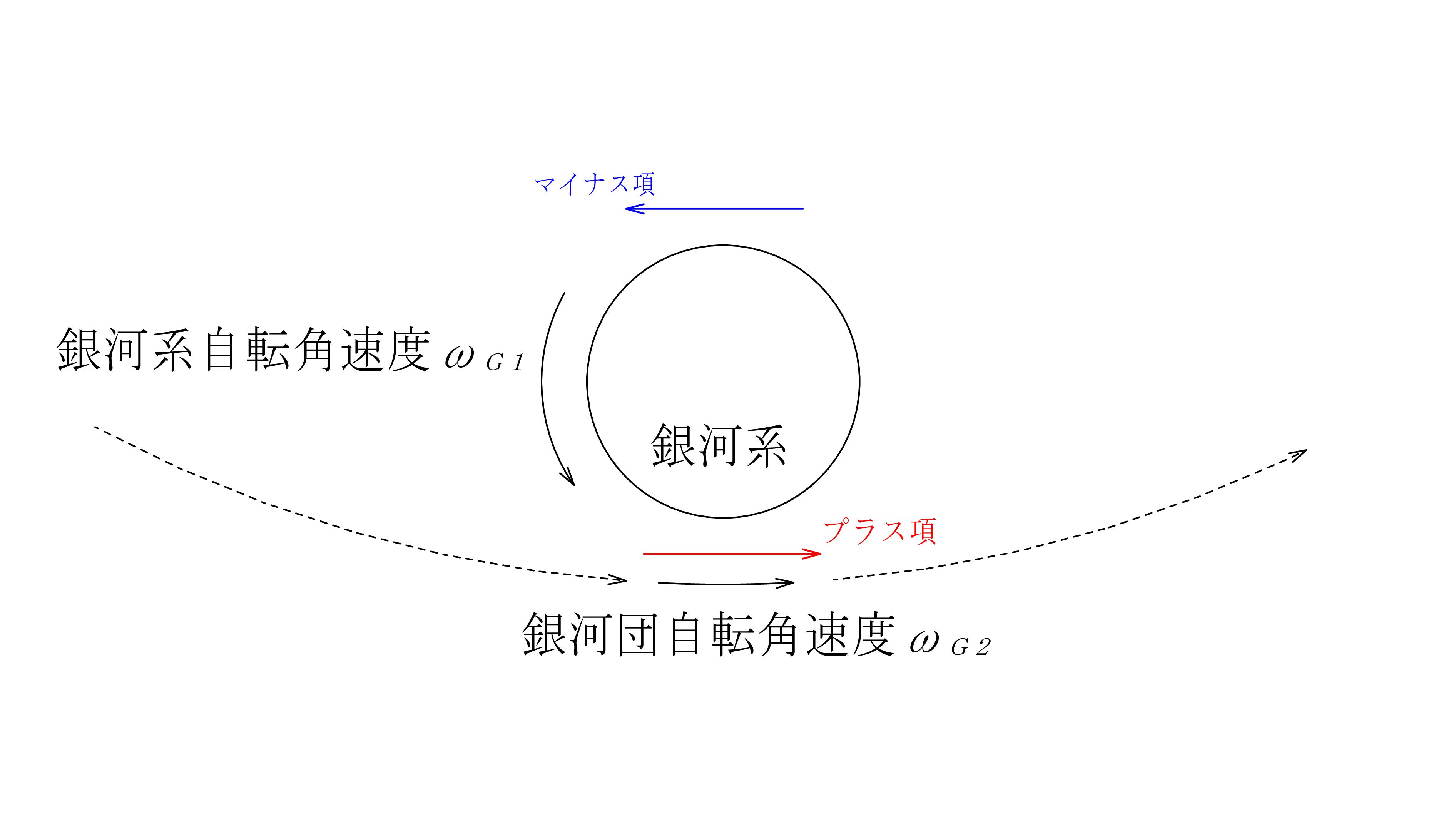
図 - 19

まとめ

回転しているコマ

カーブを走行中の電車

地球の自転

惑星の公転

地球から見える他の銀河

棒の法則