１．ボルダの振り子

解答　

１．１　重力加速度g[kg/m・s²]が生ずる理由

　重力加速度はその名のとおり地球の重力、すなわち万有引力によって生ずる加速度である。

地球が物体を引き寄せる力と、物体が地球を引き寄せる力の２の力によって生ずる。

　地球の質量をM[kg]、半径をR[m]、物体の質量をm[kg]とすれば、地球上の物体にはたらく

万有引力F[N]は、

　　　(1.1.1)

である（Gは万有引力定数G=6.67259×10^-11[N・m²/kg²]）。この力が物体にはたらく重力

であり、重力加速度をg[kg/m・s²]とすると、

F = mg　　　(1.1.2)

であるから式(1.1.1)、(1.1.2)より、

　　　(1.1.3)

である。

１．２　地上よりの高さh[m]とgとの関係

　地表での重力加速度をg[kg/m・s²]、地表からの高さh[m]での重力加速度をg’[kg/m・s²]、

地球の半径をR[m]とすると、式(1.1.3)より

　　　(1.2.1)　，　　　　　(1.2.2)

よって g’/ g は、

　　　(1.2.3)

となる。高さh[m]が地球の半径をR[m]に比べて小さいときには、次の近似式が成り立つ。

　なお、式中「〜」を上下に２つ重ねた記号は「≒（ほぼ等しい）」と同じ意味である（Wordの数式エディタ

には≒がないのである）。

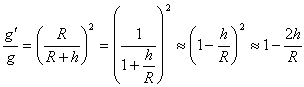　　　(1.2.4)

　式(1.2.4)から重力加速度g[kg/m・s²]は、地表からの距離h[m]が小さいときは、hの値が変化しても、

ほぼ一定の値をとる。しかし、ひじょうに高い場所ではgの値が変わる。

１．３　緯度とgとの関係

　地球の赤道半径をR[m]、赤道上での万有引力をF[N]、自転の角速度をω[rad/s]とすると、赤道上の

物体にはたらく重力mg[N]は、

mg = F - mRω²　　　(1.3.1)

となる。両極では遠心力がなく、

mg₀ = F　　　(1.3.2)

だから、式(1.3.1)、(1.3.2)より赤道上の重力加速度g[kg/m・s²]は、

g = g₀ - Rω²　　　(1.3.3)

となり、両極での重力加速度g₀[kg/m・s²]よりRω²だけ小さくなる。

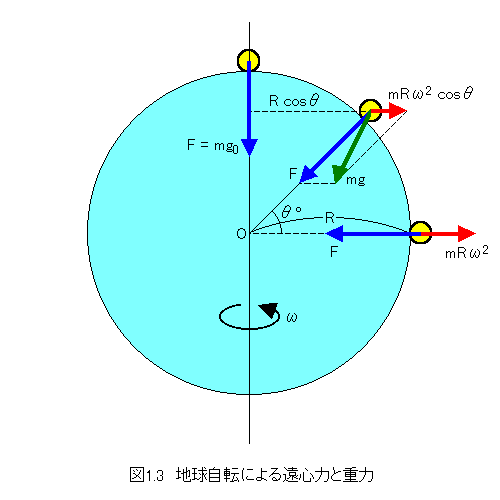
　緯度θ°の地点では自転半径が r[m] = R cosθとなるから、物体にはたらく遠心力は、

mrω² = mRω² cosθ　　　(1.3.4)

となる。この遠心力と万有引力とは同一直線上にないので、図1.3のように、平行四辺形の法則で

合成して得た力が重力となる。

　また、地上よりの高さｈや緯度のほかに重力に影響を与える原因として、地球がわずかに極方向に

つぶれた回転楕円体であることや、地球内部の密度分布の不均一性などが考えられる。

トップ