ベクトル積による
「A×B」の考察
はじめに
しづむさん、すみません。こんなページを作ってしまって(汗)。
頂いた五条義経記の案内パンフレットを読んでいたら……つい。
そのパンフレット中の「『遮那王←芥子丸』のどっちが上かわからないくらいの肉体関係」
と矢印「←」からヒントを得ました。
……どっちが上か。「←」といったらベクトル……。そうか! 「A×B」はベクトル積だったんだ!!
という具合でした(笑)。
では、無謀とも思われる考察をはじめます。
2003.01.01 Sugar
1.ベクトル積

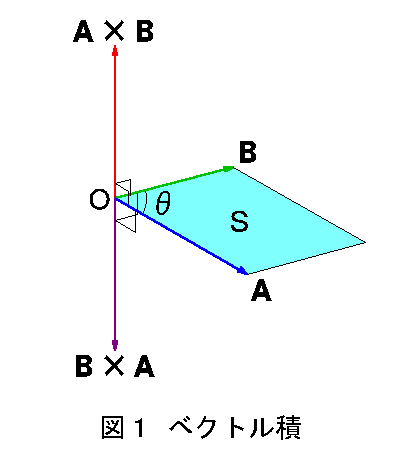
2つのベクトルA,B(以下ベクトルは太い文字で表す)があるとき、ベクトル積
C=A×B (1.1)
をつぎのように定義する。その大きさは、図1のように2つのベクトルの間の角をθとするとき、
|C|=|A×B|=S=AB sinθ (1.2)
で与えられる。向きはベクトルに垂直で、ベクトルAからBに向けて回転する右ネジの進む方向を向く。
上の定義から、掛ける順序を逆にすると、得られるベクトルは逆向きになる。すなわち、
A×B=−B×A (1.3)
となる。
2.五条義経記への置換
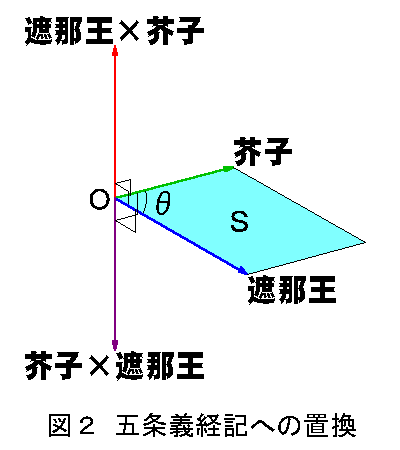
上を五条義経記の遮那王と芥子丸に置き換えると図2のようになる。図からわかるように「遮那王×芥子」と「芥子×遮那王」とは同一直線上にあり、大きさが同じ
|遮那王×芥子|=|芥子×遮那王| (2.1)
で向きが逆のベクトルとなる。点Oからそれぞれのベクトルを見ると、まったく同じに見えるのである。 あるいは、点Oに鏡を置いたと考えてもよい。
式(2.1)の絶対値記号を取り去り、ベクトル(太字)表記をやめると、
遮那王×芥子=芥子×遮那王 (2.2)
となる。この関係を別の主従関係に当てはめると、
沙門×穂邑=穂邑×沙門 (2.3)
や
朝民×伯芳=伯芳×朝民 (2.4)
などとなる。
3.ベクトル積とθ
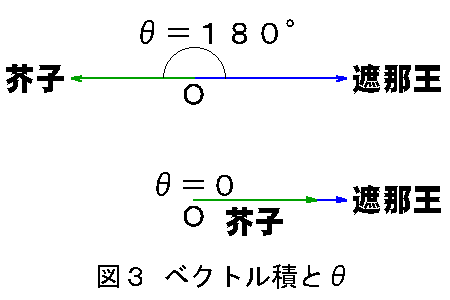
ここで、ベクトル積と2つのベクトルの間の角θについて考える。ベクトル積の大きさは、式(1.2)および図2からわかるように、遮那王と芥子を2辺とする平行四辺形の面積Sで与えられる。したがって、図3のようにθ=180°およびθ=0のときは平行四辺形ができず、ベクトル積は、
遮那王×芥子=0 (3.1)
となる。
遮那王×芥子=0でない(遮那王×芥子で萌える)ためには、それぞれの宿命のベクトルが互いに逆方向を向くことはもちろん、同一方向を向いてもいけないのである。つまり、遮那王と芥子のベクトルが微妙にずれている必要がある。
4.まとめ
以上をまとめると、つぎの2つのようになる。
まとめ1
「A(任意の人物)×B(任意の人物)」の掛ける順序を逆にすると、得られるベクトルは逆向きになる。そのベクトルの大きさ(長さ)は同じで、
A×B=B×A (4.1)
文字サイズが大きくベクトルのように見えますが、式(4.1)は
|A×B|=|B×A|を意味します。
となる。
まとめ2
「A×B」で萌えるためには、それぞれの宿命のベクトルが微妙にずれている必要がある。