丂俀亅俀丗曅懌乮帺桼搙俆乯偺塣摦曽掱幃傪夝偔丅摨偠偔廳怱偺嶼弌曽朄偺妋棫
丂
丂擇廡娫夁偓偰傑偡偹乧懯栚偠傖傫丄壌丅
丂塣摦曽掱幃偺夝朄
丂侾丗帺桼搙俇偺媟
丂傑偢丄乽懌乿偺塣摦曽掱幃傪塢乆偡傞埲慜偺栤戣偲偟偰丄乽懌乿傪儌僨儖壔偡傞偲偙傠偐傜巒傔側偄偲偄偗傑偣傫丅
丂偦傟偵偼丄傑偢1媟乮曅懌乯偺帺桼搙傪峫偊側偗傟偽側傝傑偣傫丅
丂帺桼搙偲偼偦傕偦傕丄壗偱偁傞偐偲尵偆偲丄乽帺桼偵摦偐偣傞掱搙乿偲偱傕尵偊傞偱偟傚偆偐丅
丂堦斒揑偵丄暔棟揑側儌乕僞偺悢亖帺桼搙偲尵偆擣幆偑偁傝傑偡偑丄奣偹偦偺捠傝偱偡丅傕偭偲傕丄婡峔偵傛偭偰偼暋悢偺儌乕僞偱侾帺桼搙傪埖偆偙偲傕偁傞偺偱丄堦奣偵偼婯掕偱偒傑偣傫丅
丂傑偨丄儌乕僞埲奜偺傾僋僠儏僄乕僞偵娭偟偰傕摨偠偙偲偱丄侾偮埲忋偺傾僋僠儏僄乕僞偱侾帺桼搙傪峔惉偡傞偙偲偼偁偭偰傕丄扨堦偺傾僋僠儏僄乕僞偱擇偮埲忋偺帺桼搙傪幚尰偟偨婡峔偼偁傝傑偣傫丅乮彮側偔偲傕丄巹偼暦偄偨偙偲偑偁傝傑偣傫丅乯
丂庢傝姼偊偢丄崱夞偺曕峴儘儃僢僩惢嶌偵娭偟偰偼丄暔棟揑側儌乕僞偺悢亖帺桼搙偲偄偆擣幆偱榖傪懕偗傑偡丅
丂偝偰丄恖娫偺媟偲偄偆儌僲偼丄戝傑偐偵暘偗偰丄屢娭愡丄旼娭愡丄懌庱娭愡偺俁偮偺娭愡偐傜惉偭偰偄傑偡丅乮偮傑愭偲懌偺巜偺娭愡偼丄偙偙偱偼彍奜偟偰傑偡丅乯
丂偦偟偰丄偙偺偆偪旼娭愡偼侾曽岦偵偺傒壜摦妏傪帩偮偺偱丄侾帺桼搙偱偡丅
丂懌庱偵娭偟偰偼泺偵懳偟偰慜屻丄嵍塃偺偦傟偧傟偺曽岦偵壜摦妏傪帩偪丄俀帺桼搙偲側傝傑偡丅
丂巆傝偺屢娭愡偱偡偑丄偙傟偵偮偄偰偼彮乆榖偑傗傗偙偟偔側傝傑偡丅
丂傑偢丄恖娫偺媟偼丄偮傑愭傪慜曽偵岦偗偨傑傑奐媟偑壜擻偱偡丅傑偨丄摉慠丄偮傑愭偵懳偟偰摨偠曽岦偵傕乮偮傑傝慜屻偵傕乯帺桼偵摦偐偡帠偑壜擻偱偡丅
丂偙傟偱俀帺桼搙偱偡偑丄偁偲侾偮丄恖娫偺媟乽偹偠傞乿偲偄偆摦嶌偑壜擻偱偡丅
丂偮傑愭傪擟堄偺曽岦偵岦偗偨偲偒丄晛捠偱偁傟偽旼傕摨偠曽岦偵岦偄偰偄傞敜偱偡丅
丂偙傟偼丄旼傛傝恎懱偵嬤偄晹暘丄偮傑傝屢娭愡晅嬤偵乽偹偠傞乿偲偄偆摦嶌偺帺桼搙偑懚嵼偡傞偐傜偱偡丅
丂偮傑傝丄屢娭愡偼俁帺桼搙傪帩偮帠偵側傝丄懌庱丄旼丄屢娭愡偱崌寁俇帺桼搙傪帩偮帠偵側傝傑偡丅
丂幚嵺偺恖娫乮偵尷傜偢惗暔偼奆偦偆偱偡偑乯偺媟偵偼丄嬝擏偲尵偆傾僋僠儏僄乕僞乕偑暋嶨偵攝抲偝傟偰偄傑偡偑丄俇帺桼搙偱扨弮壔偡傞偲丄恾.侾偺傛偆偵側傝傑偡丅
丂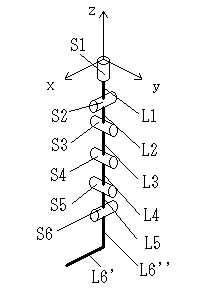
丂丂丂丂丂丂丂丂恾丏侾
丂偙偙偱丄乽俴乣乿偲偄偆偺偼丄娭愡偺娫偺嫍棧傪昞偟傑偡丅梫偼泺傗懢戁偺挿偝偲偄偆帠偱偡丅
丂傑偨乽俽乣乿偺墌摏偼丄帺桼搙偺夞揮幉傪昞偟丄偙偺墌摏偺拞怱幉偵増偭偰恾.侾偺侾媟偺儌僨儖偼夞揮塣摦傪峴偆帠偵側傝傑偡丅
丂俽侾乣俽俁偑屢娭愡丄俽係偱旼娭愡丄俽俆乣俽俇偱懌庱娫愙偵憡摉偟偰偄傑偡丅
丂偙傟偱丄媟偺儌僨儖壔偼偱偒傑偟偨丅
丂俀丗弴塣摦妛偺夝
丂偄偮偧傗偺擔婰偵傕彂偄偨巚偄傑偡偑丄弴塣摦妛夝偲偼丄娭愡傕偭偲惓妋偵尵偆側傜偽懳徾偺奺晹偺帺桼搙偺妏搙傪梌偊傞偙偲偵傛傝丄懳徾偺巔惃傪媮傔傞偙偲偱偡丅
丂偙偙偐傜愭偼丄俁師尦嵗昗忋偺儀僋僩儖偺榖偑杦偳偱丄峴楍傕弌偰偒傑偡丅偦傟傜偵娭偡傞婎慴揑側抦幆偑柍偄偲丄偐側傝擄偟偄撪梕偵側偭偰傑偡偑丄弌偰棃偨梡岅偵偮偄偰偼巹偺夝傞斖埻偱側傞傋偔愢柧偡傞條偵偟偰偒傑偡偺偱丄壜擻側尷傝丄偍晅偒崌偄偟偰傒偰壓偝偄丅
丂偲偼尵偭偰傕柍棟側恖傕嫃傞偐偲巚偄傑偡丅偦乕偄偆傂偲偼丄悋柊栻戙傢傝偵偟偰壓偝偄丅乮丱丱丟
丂傑偢丄慜崁偺媟傪儌僨儖壔偟偨恾.侾偐傜丄儀僋僩儖恾傪嶌傝傑偡丅乮恾.俀乯
丂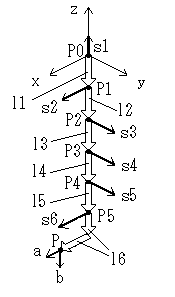
丂丂丂丂丂丂丂丂恾丏俀
丂恾.俀偼婎弨巔惃偵偍偗傞儀僋僩儖恾偱偡丅乽俹乣乿偼奺儕儞僋晹偺埵抲儀僋僩儖丄乽l乣乿偼儕儞僋娫偺儀僋僩儖丄乽倱乣乿偼奺帺桼搙偺夞揮幉偺曽岦傪昞偡扨埵儀僋僩儖偱偡丅
丂乮扨埵儀僋僩儖偲偼丄儀僋僩儖偺挿偝偑侾乮嵟彫扨埵乯偱丄曽岦偺傒傪昞偟偨儀僋僩儖偱偡丅乯
丂彯丄乽a乿偼偮傑愭偺曽岦傪昞偡扨埵儀僋僩儖丄乽b乿偼儀僋僩儖乽a乿偺巔惃傪昞偡儀僋僩儖乧偲偄偆偐丄偙偺応崌偼懌棤偺曽岦傪昞偡扨埵儀僋僩儖偩偲峫偊偰栤戣偁傝傑偣傫丅
丂偝偰丄偙偙偱婎弨埵抲偵偍偗傞偦傟偧傟偺儀僋僩儖傪尒偰傒傑偡丅
丂丂丂丂丂丂丂丂丂乷倶嵗昗乸
丂儀僋僩儖丂亖丂乷倷嵗昗乸丂丂丂丂亖丂乮倶嵗昗丄倄嵗昗丄倸嵗昗乯俿
丂丂丂丂丂丂丂丂丂乷倸嵗昗乸
丂偲偡傞偲丄
丂倢侾丂亖丂乮侽丄侽丄亅俴侾乯俿
丂倢俀丂亖丂乮侽丄侽丄亅俴俀乯俿
丂倢俁丂亖丂乮侽丄侽丄亅俴俁乯俿
丂倢係丂亖丂乮侽丄侽丄亅俴係乯俿
丂倢俆丂亖丂乮侽丄侽丄亅俴俆乯俿
丂倢俇丂亖丂乮俴俇'丄侽丄亅俴俇乫乫乯俿
丂倎丂亖丂乮侾丄侽丄侽乯俿
丂倐丂亖丂乮侽丄侽丄亅侾乯俿
丂偲側傝傑偡丅
丂偙偙偐傜偑弴塣摦妛夝愅偱偡丅
丂傑偢丄媟偺愭抂乮偮傑愭乯傪昞偡儀僋僩儖乽俹乿傪帵偡儀僋僩儖曽掱幃傪峫偊傑偡丅
丂偙傟偼偛偔娙扨偵丄倢侾乣倢俇傑偱偺儀僋僩儖傪崌寁偡傟偽媮傑傝傑偡丅
丂扐偟丄婎弨埵抲偱偁傟偽忋婰偺倢侾乣倢俇傑偱傪崌寁偡傟偽俷俲偱偡偑丄幚嵺偺摦嶌拞偵偼摉慠丄奺儕儞僋偺夞揮幉偵偼偦傟偧傟偺妏搙偑梌偊傜傟偰偄傑偡丅偦偺夞揮暘傪峫椂偟側偗傟偽丄惓偟偄巔惃偼媮傑傝傑偣傫丅
丂偦偙偱昁梫偵側偭偰偔傞偺偑丄夞揮曄姺峴楍俤乮冎兤乯偱偡丅
丂偁傞儀僋僩儖俙亖乮俙倶丄俙倷丄俙倸乯俿偑俁師尦嵗昗忋偺倸幉廃傝偵兤偩偗夞揮偟偨偲偒偺儀僋僩儖傪俙乫偲偡傞偲丄
丂俙乫丂亖丂俤乮倠兤乯俙
丂丂丂丂丂丂丂丂丂 乷丂俠兤丂亅俽兤丂 侽乸
丂俤乮倠兤乯丂亖丂乷丂俽兤丂丂俠兤丂丂侽乸
丂丂丂丂丂丂丂丂丂 乷丂丂侽丂丂丂侽丂丂丂侾乸
丂扐偟丄
丂俽兤丂亖丂倱倝値兤
丂俠兤丂亖丂們倧倱兤
丂偲偄偆娭學偑偁傝傑偡丅
丂偙偺俤乮倠兤乯傪倠幉乮倸幉乯夞傝偺夞揮曄姺峴楍偲尵偄傑偡丅
丂摨條偵丄倝幉乮倶幉乯丄倞幉乮倷幉乯夞傝偺夞揮曄姺峴楍傕丄
丂丂丂丂丂丂丂丂丂乷丂丂侾丂丂丂侽丂丂丂丂侽乸
丂俤乮倝兤乯丂亖丂 乷丂丂侽丂丂俠兤丂亅俽兤乸
丂丂丂丂丂丂丂丂丂乷丂丂侽丂丂俽兤丂丂俠兤乸
丂丂丂丂丂丂丂丂丂乷丂俠兤丂丂丂侽丂丂俽兤乸
丂俤乮倞兤乯丂亖丂乷丂丂侽丂丂丂丂侾丂丂丂侽乸
丂丂丂丂丂丂丂丂丂乷亅俽兤丂丂 侽丂丂俠兤乸
丂偲媮傔傜傟傑偡丅
丂偙傟傪峫椂偟偰俹偵娭偡傞儀僋僩儖曽掱幃傪棫偰傞偲丄
丂俹丂亖丂俤乮倠兤侾乯倢侾丂亄丂俤乮倠兤侾乯俤乮倝兤俀乯倢俀丂亄丂俤乮倠兤侾乯俤乮倝兤俀乯俤乮倞兤俁乯倢俁丂亄丂俤乮倠兤侾乯俤乮倝兤俀乯俤乮倞兤俁乯俤乮倞兤係乯倢係
丂丂丂丂丂亄丂俤乮倠兤侾乯俤乮倝兤俀乯俤乮倞兤俁乯俤乮倞兤係乯俤乮倞兤俆乯倢俆丂亄丂俤乮倠兤侾乯俤乮倝兤俀乯俤乮倞兤俁乯俤乮倞兤係乯俤乮倞兤俆乯俤乮倝兤俇乯倢俇丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂乮侾乯
丂俹丂亖丂俼乮侾乯倢侾丂亄丂俼乮俀乯倢俀丂亄丂俼乮俁乯倢俁丂亄丂俼乮係乯倢係丂亄丂俼乮俆乯倢俆丂亄丂俼乮俇乯倢俇丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂乮俀乯
丂偲側傝傑偡丅
丂梫偼丄擟堄偺儕儞僋揰俹乣偵塭嬁傪媦傏偡妏搙傪峫椂偟偰偄傞丄偲尵偆帠偱偡丅
丂椺偊偽丄堦斣崻尦偺俹侾偱偼丄峫椂偡傞偺偼帺恎偺夞揮妏兤侾偺傒偱椙偄帠偵側傝傑偡丅乮崱夞偺応崌偼丄夞揮幉偲倢侾偺曽岦偑摨偠側堊丄幚嵺偵偼俹侾偺埵抲偵偼兤侾偼娭學偁傝傑偣傫偑乯
丂師偺俹俀偱偼丄婎弨埵抲偱偼夞揮幉偼倶幉偲摨偠曽岦偱偡偑丄兤侾偑壖偵俋侽亱夞揮偟偰偄偨偲偡傟偽丄倱俀偼倷幉偺曽岦傪岦偄偰偄傞偙偲偵側傝傑偡丅
丂峏偵師偺俹俁偱偼丄兤侾丄兤俀偺妏搙丄俹係偱偼兤侾丄兤俀丄兤俁偺妏搙乧偲偄偆條偵丄愭抂偵側傞傎偳丄偦偺儕儞僋傛傝崻尦偵嬤偄儕儞僋偺夞揮妏偺塭嬁傪庴偗偰偄偒傑偡丅
丂偙傟偼傓偟傠摉慠偲尵偊偽摉慠偺偙偲偱丄姶妎揑偵暘偐傝堈偄偲巚偄傑偡丅
丂偱偼丄幚嵺偵俼乮乣乯傪媮傔偰傒傑偡丅
丂枖偙偙偱丄俴俀偲俴俆傪侽偲偟傑偡丅乮俽俀偲俽俁丄俽俆偲俽俇偺夞揮幉傪偦傟偧傟摨偠埵抲偵偡傞堊偱偡丅偙偺曽偑丄寁嶼偼妝偵側傞偐傜偱偡乯
丂峏偵丄棟桼偼屻弎偟傑偡偑丄俴俁亖俴係偲偟傑偡丅
丂傛偭偰丄乮俀乯偼丄
丂俹丂亖丂俼乮侾乯倢侾丂亄丂俼乮俁乯倢俁丂亄丂俼乮係乯倢係丂亄丂俼乮俇乯倢俇丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂乮俀乫乯
偲曄宍偝傟傑偡丅
丂丂丂丂丂丂丂丂丂丂乷丂俠侾丂亅俽侾丂 侽乸乷丂侽丂乸
丂俼乮侾乯倢侾丂亖丂 乷丂俽侾丂丂俠侾丂丂侽乸乷丂侽丂乸
丂丂丂丂丂丂丂丂丂丂乷丂丂侽丂丂丂侽丂丂侾乸乷亅俴侾乸
丂丂丂丂丂丂丂丂丂丂乷丂侽丂乸
丂俼乮侾乯倢侾丂亖丂 乷丂侽丂乸丂丂丂丂丂丂丂丂丂丂乮俁乯
丂丂丂丂丂丂丂丂丂丂乷亅俴侾乸
丂丂丂丂丂丂丂丂丂丂乷丂俠侾丂亅俽侾丂 侽乸乷丂丂侾丂丂丂侽丂丂丂丂侽乸乷丂侽丂乸
丂俼乮俀乯倢俀丂亖丂 乷丂俽侾丂丂俠侾丂丂侽乸乷丂丂侽丂丂俠俀丂亅俽俀乸乷丂侽丂乸
丂丂丂丂丂丂丂丂丂丂乷丂丂侽丂丂丂侽丂丂侾乸乷丂丂侽丂丂俽俀丂丂丂俠俀乸乷亅俴俀乸
丂扐偟丄俴俀丂亖丂侽偺偨傔丄
丂俼乮俀乯倢俀丂亖丂侽丂丂丂丂丂丂丂丂丂丂乮係乯
丂丂丂丂丂丂丂丂丂丂乷丂俠侾丂亅俽侾丂 侽乸乷丂丂侾丂丂丂侽丂丂丂丂侽乸乷丂俠俁丂丂丂侽丂丂俽俁乸乷丂侽丂乸
丂俼乮俁乯倢俁丂亖丂 乷丂俽侾丂丂俠侾丂丂侽乸乷丂丂侽丂丂俠俀丂亅俽俀乸乷丂 侽丂丂丂丂侾丂丂丂侽乸乷丂侽丂乸
丂丂丂丂丂丂丂丂丂丂乷丂丂侽丂丂丂侽丂丂侾乸乷丂丂侽丂丂俽俀丂丂丂俠俀乸乷亅俽俁丂丂 侽丂丂俠俁乸乷亅俴俁乸
丂丂丂丂丂丂丂丂丂丂乷亅俠侾俽俁亅俽侾俽俀俠俁乸
丂俼乮俁乯倢俁丂亖丂 乷亅俽侾俽俁亄俠侾俽俀俠俁乸俴俁丂丂丂丂丂丂丂丂丂丂乮俆乯
丂丂丂丂丂丂丂丂丂丂乷亅俠俀俠俁丂丂丂丂丂丂丂 乸
丂丂丂丂丂丂丂丂丂丂乷丂俠侾丂亅俽侾丂 侽乸乷丂丂侾丂丂丂侽丂丂丂丂侽乸乷丂俠俁丂丂丂侽丂丂俽俁乸乷丂俠係丂丂丂侽丂丂俽係乸乷丂侽丂乸
丂俼乮係乯倢係丂亖丂 乷丂俽侾丂丂俠侾丂丂侽乸乷丂丂侽丂丂俠俀丂 亅俽俀乸乷丂 侽丂丂丂丂侾丂丂 侽乸乷丂 侽丂丂丂丂侾丂丂丂侽乸乷丂侽丂乸
丂丂丂丂丂丂丂丂丂丂乷丂丂侽丂丂丂侽丂丂侾乸乷丂丂侽丂丂俽俀丂丂丂俠俀乸乷亅俽俁丂丂 侽丂丂俠俁乸乷亅俽係丂丂 侽丂丂俠係乸乷亅俴係乸
丂丂丂丂丂丂丂丂丂丂乷亅俠侾俽乮俁亄係乯亅俽侾俽俀俠乮俁亄係乯乸
丂俼乮係乯倢係丂亖丂 乷亅俽侾俽乮俁亄係乯亄俠侾俽俀俠乮俁亄係乯乸俴係丂丂丂丂丂丂丂丂丂丂乮俇乯
丂丂丂丂丂丂丂丂丂丂乷亅俠俀俠乮俁亄係乯丂丂丂丂丂丂丂丂丂丂丂 乸
丂丂丂丂丂丂丂丂丂丂乷丂俠侾丂亅俽侾丂 侽乸乷丂丂侾丂丂丂侽丂丂丂丂侽乸乷丂俠俁丂丂丂侽丂丂俽俁乸乷丂俠係丂丂丂侽丂丂俽係乸乷丂俠俆丂丂丂侽丂丂俽俆乸乷丂侽丂乸
丂俼乮俆乯倢俆丂亖丂 乷丂俽侾丂丂俠侾丂丂侽乸乷丂丂侽丂丂俠俀丂 亅俽俀乸乷丂 侽丂丂丂丂侾丂丂 侽乸乷丂 侽丂丂丂丂侾丂丂丂 侽乸乷丂 侽丂丂丂丂侾丂丂 侽乸乷丂侽丂乸
丂丂丂丂丂丂丂丂丂丂乷丂丂侽丂丂丂侽丂丂侾乸乷丂丂侽丂丂俽俀丂丂丂俠俀乸乷亅俽俁丂丂 侽丂丂俠俁乸乷亅俽係丂丂 侽丂丂俠係乸乷亅俽俆丂丂 侽丂丂俠俆乸乷亅俴俆乸
丂扐偟丄俴俆丂亖丂侽偺偨傔丄
丂俼乮俆乯倢俆丂亖丂侽丂丂丂丂丂丂丂丂丂丂乮俈乯
丂丂丂丂丂丂丂丂丂丂乷丂俠侾丂亅俽侾丂 侽乸乷丂丂侾丂丂丂侽丂丂丂丂侽乸乷丂俠俁丂丂丂侽丂丂俽俁乸乷丂俠係丂丂丂侽丂丂俽係乸乷丂俠俆丂丂丂侽丂丂俽俆乸乷丂丂侾丂丂丂侽丂丂丂丂侽乸乷俴俇乫乸
丂俼乮俇乯倢俇丂亖丂 乷丂俽侾丂丂俠侾丂丂侽乸乷丂丂侽丂丂俠俀丂 亅俽俀乸乷丂 侽丂丂丂丂侾丂丂 侽乸乷丂 侽丂丂丂丂侾丂丂丂 侽乸乷丂 侽丂丂丂丂侾丂丂 侽乸乷丂丂侽丂丂俠俇丂 亅俽俇乸乷丂侽丂乸
丂丂丂丂丂丂丂丂丂丂乷丂丂侽丂丂丂侽丂丂侾乸乷丂丂侽丂丂俽俀丂丂丂俠俀乸乷亅俽俁丂丂 侽丂丂俠俁乸乷亅俽係丂丂 侽丂丂俠係乸乷亅俽俆丂丂 侽丂丂俠俆乸乷丂丂侽丂丂俽俇丂丂丂俠俇乸乷亅俴俇乫乫乸
丂丂丂丂丂丂丂丂丂丂乷俠侾俠乮俁亄係亄俆乯亅俽侾俽俀俽乮俁亄係亄俆乯乸丂丂丂丂丂丂乷亅俠侾俽乮俁亄係亄俆乯俠俇亅俽侾俠俀俽俇亅俽侾俽俀俠乮俁亄係亄俆乯俠俇乸
丂俼乮俇乯倢俇丂亖丂 乷俽侾俠乮俁亄係亄俆乯亄俠侾俽俀俽乮俁亄係亄俆乯乸俴俇乫丂亄丂乷亅俽侾俽乮俁亄係亄俆乯俠俇亄俠侾俠俀俽俇亄俠侾俽俀俠乮俁亄係亄俆乯俠俇乸俴俇乫乫丂丂丂丂丂丂丂丂乮俉乯
丂丂丂丂丂丂丂丂丂丂乷亅俠俀俽乮俁亄係亄俆乯丂丂丂丂丂丂丂丂丂丂丂丂丂乸丂丂丂丂丂丂乷俽俀俽俇亅俠俀俠乮俁亄係亄俆乯俠俇丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂乸
丂傑偨丄倎丄倐傪媮傔傞偲丄
丂丂丂丂丂丂乷丂俠侾丂亅俽侾丂 侽乸乷丂丂侾丂丂丂侽丂丂丂丂侽乸乷丂俠俁丂丂丂侽丂丂俽俁乸乷丂俠係丂丂丂侽丂丂俽係乸乷丂俠俆丂丂丂侽丂丂俽俆乸乷丂丂侾丂丂丂侽丂丂丂丂侽乸乷丂侾丂乸
丂倎丂亖丂 乷丂俽侾丂丂俠侾丂丂侽乸乷丂丂侽丂丂俠俀丂 亅俽俀乸乷丂 侽丂丂丂丂侾丂丂 侽乸乷丂 侽丂丂丂丂侾丂丂丂 侽乸乷丂 侽丂丂丂丂侾丂丂 侽乸乷丂丂侽丂丂俠俇丂 亅俽俇乸乷丂侽丂乸
丂丂丂丂丂丂乷丂丂侽丂丂丂侽丂丂侾乸乷丂丂侽丂丂俽俀丂丂丂俠俀乸乷亅俽俁丂丂 侽丂丂俠俁乸乷亅俽係丂丂 侽丂丂俠係乸乷亅俽俆丂丂 侽丂丂俠俆乸乷丂丂侽丂丂俽俇丂丂丂俠俇乸乷丂侽丂乸
丂丂丂丂丂丂乷俠侾俠乮俁亄係亄俆乯亅俽侾俽俀俽乮俁亄係亄俆乯乸
丂倎丂亖丂 乷俽侾俠乮俁亄係亄俆乯亄俠侾俽俀俽乮俁亄係亄俆乯乸丂丂丂丂丂丂丂丂丂丂丂丂乮俋乯
丂丂丂丂丂丂乷亅俠俀俽乮俁亄係亄俆乯丂丂丂丂丂丂丂丂丂丂丂丂 乸
丂丂丂丂丂丂乷丂俠侾丂亅俽侾丂 侽乸乷丂丂侾丂丂丂侽丂丂丂丂侽乸乷丂俠俁丂丂丂侽丂丂俽俁乸乷丂俠係丂丂丂侽丂丂俽係乸乷丂俠俆丂丂丂侽丂丂俽俆乸乷丂丂侾丂丂丂侽丂丂丂丂侽乸乷丂侽丂乸
丂倐丂亖丂 乷丂俽侾丂丂俠侾丂丂侽乸乷丂丂侽丂丂俠俀丂 亅俽俀乸乷丂 侽丂丂丂丂侾丂丂 侽乸乷丂 侽丂丂丂丂侾丂丂丂 侽乸乷丂 侽丂丂丂丂侾丂丂 侽乸乷丂丂侽丂丂俠俇丂 亅俽俇乸乷丂侽丂乸
丂丂丂丂丂丂乷丂丂侽丂丂丂侽丂丂侾乸乷丂丂侽丂丂俽俀丂丂丂俠俀乸乷亅俽俁丂丂 侽丂丂俠俁乸乷亅俽係丂丂 侽丂丂俠係乸乷亅俽俆丂丂 侽丂丂俠俆乸乷丂丂侽丂丂俽俇丂丂丂俠俇乸乷亅1丂乸
丂丂丂丂丂丂乷亅俠侾俽乮俁亄係亄俆乯俠俇亅俽侾俠俀俽俇亅俽侾俽俀俠乮俁亄係亄俆乯俠俇乸
丂倐丂亖丂 乷亅俽侾俽乮俁亄係亄俆乯俠俇亄俠侾俠俀俽俇亄俠侾俽俀俠乮俁亄係亄俆乯俠俇乸丂丂丂丂丂丂丂丂丂丂乮侾侽乯
丂丂丂丂丂丂乷俽俀俽俇亅俠俀俠乮俁亄係亄俆乯俠俇丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 乸
丂夝偄偰傒傞偲丄倎丄倐偼偦傟偧傟倢俇偺俴俇乫丄俴俇乫乫偺惉暘偺扨埵儀僋僩儖偱偁傞偙偲偑暘傞偲巚偄傑偡丅
丂師偵丄夞揮幉儀僋僩儖倱侾乣倱俇傪偦傟偧傟媮傔傑偡丅
丂媮傔曽偼婎杮揑偵丂俼乮乣乯倢乣丂偲摨偠偱偡丅
丂梫偼偦偺夞揮幉偵塭嬁傪梌偊傞儕儞僋傪峫椂偟偰幃傪棫偰傠丄偲偄偆偙偲偱偡偹丅
丂乧偲偄偆偐丄媮傔曽偳偙傠偐丄幃帺懱傕杦偳摨偠側傫偱偡偑丅
奺夞揮幉儀僋僩儖偺夝
丂丂丂丂丂丂 乷丂俠侾丂亅俽侾丂 侽乸乷丂侽丂乸
丂倱侾丂亖丂乷丂俽侾丂丂俠侾丂丂侽乸乷丂侽丂乸
丂丂丂丂丂丂 乷丂丂侽丂丂丂侽丂丂侾乸乷丂侾丂乸
丂丂丂丂丂丂 乷丂侽丂乸
丂倱侾丂亖丂乷丂侽丂乸丂丂丂丂丂丂丂丂丂丂乮侾侾乯
丂丂丂丂丂丂 乷丂侾丂乸
丂丂丂丂丂丂 乷丂俠侾丂亅俽侾丂 侽乸乷丂丂侾丂丂丂侽丂丂丂丂侽乸乷丂侾丂乸
丂倱俀丂亖丂乷丂俽侾丂丂俠侾丂丂侽乸乷丂丂侽丂丂俠俀丂 亅俽俀乸乷丂侽丂乸
丂丂丂丂丂丂 乷丂丂侽丂丂丂侽丂丂侾乸乷丂丂侽丂丂俽俀丂丂丂俠俀乸乷丂侽丂乸
丂丂丂丂丂丂 乷丂俠侾乸
丂倱俀丂亖丂乷丂俽侾乸丂丂丂丂丂丂丂丂丂丂乮侾俀乯
丂丂丂丂丂丂 乷丂侽丂乸
丂丂丂丂丂丂 乷丂俠侾丂亅俽侾丂 侽乸乷丂丂侾丂丂丂侽丂丂丂丂侽乸乷丂俠俁丂丂丂侽丂丂俽俁乸乷丂侽丂乸
丂倱俁丂亖丂乷丂俽侾丂丂俠侾丂丂侽乸乷丂丂侽丂丂俠俀丂 亅俽俀乸乷丂 侽丂丂丂 侾丂丂丂侽乸乷丂侾丂乸
丂丂丂丂丂丂 乷丂丂侽丂丂丂侽丂丂侾乸乷丂丂侽丂丂俽俀丂丂丂俠俀乸乷亅俽俁丂丂 侽丂丂俠俁乸乷丂侽丂乸
丂丂丂丂丂丂 乷亅俽侾俠俀乸
丂倱俁丂亖丂乷丂 俠侾俠俀乸丂丂丂丂丂丂丂丂丂丂乮侾俁乯
丂丂丂丂丂丂 乷丂丂俽俀丂 乸
丂丂丂丂丂丂 乷丂俠侾丂亅俽侾丂 侽乸乷丂丂侾丂丂丂侽丂丂丂丂侽乸乷丂俠俁丂丂丂侽丂丂俽俁乸乷丂俠係丂丂丂侽丂丂俽係乸乷丂侽丂乸
丂倱係丂亖丂乷丂俽侾丂丂俠侾丂丂侽乸乷丂丂侽丂丂俠俀丂 亅俽俀乸乷丂 侽丂丂丂丂侾丂丂 侽乸乷丂 侽丂丂丂丂侾丂丂丂侽乸乷丂侾丂乸
丂丂丂丂丂丂 乷丂丂侽丂丂丂侽丂丂侾乸乷丂丂侽丂丂俽俀丂丂丂俠俀乸乷亅俽俁丂丂 侽丂丂俠俁乸乷亅俽係丂丂 侽丂丂俠係乸乷丂侽丂乸
丂丂丂丂丂丂 乷亅俽侾俠俀乸
丂倱係丂亖丂乷丂 俠侾俠俀乸丂丂丂丂丂丂丂丂丂丂乮侾係乯
丂丂丂丂丂丂 乷丂丂俽俀丂 乸
丂丂丂丂丂丂 乷丂俠侾丂亅俽侾丂 侽乸乷丂丂侾丂丂丂侽丂丂丂丂侽乸乷丂俠俁丂丂丂侽丂丂俽俁乸乷丂俠係丂丂丂侽丂丂俽係乸乷丂俠俆丂丂丂侽丂丂俽俆乸乷丂侽丂乸
丂倱俆丂亖丂乷丂俽侾丂丂俠侾丂丂侽乸乷丂丂侽丂丂俠俀丂 亅俽俀乸乷丂 侽丂丂丂丂侾丂丂 侽乸乷丂 侽丂丂丂丂侾丂丂丂 侽乸乷丂 侽丂丂丂丂侾丂丂 侽乸乷丂侾丂乸
丂丂丂丂丂丂 乷丂丂侽丂丂丂侽丂丂侾乸乷丂丂侽丂丂俽俀丂丂丂俠俀乸乷亅俽俁丂丂 侽丂丂俠俁乸乷亅俽係丂丂 侽丂丂俠係乸乷亅俽俆丂丂 侽丂丂俠俆乸乷丂侽丂乸
丂丂丂丂丂丂 乷亅俽侾俠俀乸
丂倱俆丂亖丂乷丂 俠侾俠俀乸丂丂丂丂丂丂丂丂丂丂乮侾俆乯
丂丂丂丂丂丂 乷丂丂俽俀丂 乸
丂丂丂丂丂丂 乷丂俠侾丂亅俽侾丂 侽乸乷丂丂侾丂丂丂侽丂丂丂丂侽乸乷丂俠俁丂丂丂侽丂丂俽俁乸乷丂俠係丂丂丂侽丂丂俽係乸乷丂俠俆丂丂丂侽丂丂俽俆乸乷丂丂侾丂丂丂侽丂丂丂丂侽乸乷丂侾丂乸
丂倱俇丂亖丂乷丂俽侾丂丂俠侾丂丂侽乸乷丂丂侽丂丂俠俀丂 亅俽俀乸乷丂 侽丂丂丂丂侾丂丂 侽乸乷丂 侽丂丂丂丂侾丂丂丂 侽乸乷丂 侽丂丂丂丂侾丂丂 侽乸乷丂丂侽丂丂俠俇丂 亅俽俇乸乷丂侽丂乸
丂丂丂丂丂丂 乷丂丂侽丂丂丂侽丂丂侾乸乷丂丂侽丂丂俽俀丂丂丂俠俀乸乷亅俽俁丂丂 侽丂丂俠俁乸乷亅俽係丂丂 侽丂丂俠係乸乷亅俽俆丂丂 侽丂丂俠俆乸乷丂丂侽丂丂俽俇丂丂丂俠俇乸乷丂侽丂乸
丂丂丂丂丂丂 乷俠侾俠乮俁亄係亄俆乯亅俽侾俽俀俽乮俁亄係亄俆乯乸
丂倱俇丂亖丂乷俽侾俠乮俁亄係亄俆乯亄俠侾俽俀俽乮俁亄係亄俆乯乸丂丂丂丂丂丂丂丂丂丂丂丂丂丂乮侾俇乯
丂丂丂丂丂丂 乷亅俠俀俽乮俁亄係亄俆乯丂丂丂丂丂丂丂丂丂丂丂丂 乸
丂夞揮幉儀僋僩儖偼丄夞揮幉偺曽岦傪昞偡儀僋僩儖偱偁傝丄埵抲傗嫍棧傪帵偡傕偺偱偼偁傝傑偣傫丅俴乣偺惉暘傪娷傫偱偄側偄偺偼偦偺堊偱偡丅
丂埲忋偺偙偲偵偮偄偰丄乽暘傞偐儃働両乿偲偐尵偆曽偼丄偲偵偐偔幃乮俁乯乣乮侾俇乯偱弴塣摦妛偑夝偗偨偲偄偆偙偲偩偗壇偊偰偍偄偰壓偝偄丅
丂俁丗媡塣摦妛偺夝
丂媡塣摦妛偺栤戣偺夝寛偼丄婔壗妛偺夝寛偵帡偰捈姶揑側偲偙傠偑偁傝丄堦掕偺夝朄偼側偄丅傑偨偡傋偰偺婡峔偵偮偄偰傕媡塣摦妛偑夝偗傞傢偗偱傕側偄丅偟偐偟丄尰忬偱偼偙偺夝偺桿摫偼晄壜寚偱偁傞丅側偤側傜捠忢巊梡偝傟偰偄傞儅僯僺儏儗乕僞偺応崌乧乧
丂乮嶲峫恾彂丗儘儃僢僩岺妛乮夵掶斉乯丂峀悾栁抝挊丄徶壺朳傛傝敳悎乯
丂梫偼姶妎偑戝帠丄偲偄偆偙偲偱偟傚偆偐丅乮偪傚偭偲堘偆乯
丂幚嵺丄峴楍幃偲偵傜傔偭偙偡傞傛傝傕丄帺暘偺懌傪怳傝夞偟側偑傜峫偊傞帪娫偺曽偑挿偐偭偨偱偡丅
丂乽偮傑愭偺埵抲傗巔惃傪妋掕偟偨傜丄杮摉偵懌庱傗旼丄屢娭愡偺妏搙偑寛傑傞偺偩傠偆偐丠乿
丂側偳偲帺栤帺摎傪孞傝曉偟傑偟偨偑丄傛偆傗偭偲乮曅懌暘偺媡塣摦妛夝偼乯夝偗傑偟偨丅
丂杮崁偺彉暥偵偁偭偨傛偆偵丄媡塣摦妛栤戣偺夝偒曽偵偼堦掕偺夝朄偼偁傝傑偣傫丅
丂偙偙偱徯夘偡傞偺偼丄巹偑柍偄傾僞儅傪偙偹偔傝夞偟偰摫偄偨夝朄偱偁傝丄傕偭偲岠棪偺椙偄夝朄偑懚嵼偡傞壜擻惈偼廫暘偵偁傝傑偡丅
丂柕弬揰丄媈栤丄幙栤偑偁傝傑偟偨傜丄偳偟偳偟偍婑偣壓偝偄丅
丂偝偰丄慜崁偱俇帺桼搙偺媟偺弴塣摦妛傪夝偄偨栿偱偡偑丄師偼偦偺媡丄偮傑愭偺埵抲偲巔惃傪梌偊偰丄奺儕儞僋偺夞揮妏傪媮傔傑偡丅
丂嵟弶偵婛抦偱偁傞僷儔儊乕僞傪惍棟偟傑偡丅
丂侾丗倎亖乮倎倶丄倎倷丄倎倸乯俿
丂丂丂偮傑愭偺岦偄偰偄傞曽岦傪帵偟傑偡丅擟堄偺抣傪梌偊傑偡丅
丂俀丗倐亖乮倐倶丄倐倷丄倐倸乯俿
丂丂丂儀僋僩儖倎帺懱偺巔惃乧偲偄偆偐偙偺応崌偼懌棤偺曽岦傪帵偡偲偟偨曽偑暘偐傝堈偄偱偟傚偆丅
丂丂丂偙傟傑偨丄擟堄抣傪梌偊傑偡偑丄慜採偲偟偰儀僋僩儖倎偵捈岎偡傞儀僋僩儖偱偁傞帠偑昁恵忦審偲側傝傑偡丅乮暔棟揑偵偦偆偄偆峔憿偱峫偊偰偄傞堊乯
丂俁丗俹亖乮俹倶丄俹倷丄俹倸乯俿
丂丂丂偮傑愭偺埵抲傪帵偟傑偡丅崱夞偺応崌乮侾媟偺傒偺応崌乯偼尨揰乮媟偺崻尦乯偐傜偺埵抲偵側傝傑偡丅
丂丂丂摉偨傝慜偱偡偑丄媟傪堦攖偵怢偽偟偨嫍棧傛傝墦偄揰偱偼夝偼摼傜傟側偄偺偱丄乽偮傑愭偺撏偔斖埻偺埵抲乿偲偄偆偺偑昁恵忦審偱偡丅
丂係丗俴侾乣俴俆丄俴俇乫丄俴俇乫乫偺挿偝
丂丂丂媟偺奺晹偺悺朄偱偡丅愝寁帪偵寛掕偝傟傑偡丅摉慠丄尰幚揑側抣偱偡丅
丂埲忋偺婛抦抣偐傜丄慜崁偱摫弌偟偨幃傕梡偄偰丄兤侾乣兤俇傪媮傔傞帠偵側傝傑偡丅
嘥丗兤侾摫弌
丂傑偢丄兤侾偺摫弌偐傜巒傔傞帠偵偟傑偡丅
丂偙偙偱拲栚偟偨偄偺偼丄夞揮幉儀僋僩儖倱俁乣倱俆偱偡丅
丂慜崁偱摫弌偟偨捠傝丄偙偺俁偮偺儀僋僩儖偼慡偔摨偠夝偵側傝傑偡丅
丂偙傟偼丄偙偺俁偮偺儀僋僩儖偑丄婡峔忋偺棟桼偐傜忢偵暯峴偵側傞偨傔偱丄倱俆偑敾柧偡傟偽帺摦揑偵倱俁傑偱妋掕偱偒傞偙偲偵側傝傑偡丅
丂偙偺倱俆偼丄
丂倱俆丂亖丂乮倱俆倶丄倱俆倷丄倱俆倸乯俿丂亖丂乮亅俽侾俠俀丄俠侾俠俀丄俽俀乯俿
丂偱偁傝丄
丂丂丂丂丂丂丂丂丂-侾丂丂丂俽侾丂丂丂丂丂丂丂-侾丂丂丂亅乮亅俽侾俠俀乯
丂兤侾丂亖丂倲倎値丂丂丂乮乗乗乗乯丂亖丂倲倎値丂丂乮乗乗乗乗乗乗乗乗乯
丂丂丂丂丂丂丂丂丂丂丂丂丂丂俠侾丂丂丂丂丂丂丂丂丂丂丂丂丂丂俠侾俠俀
丂丂丂丂丂丂丂丂丂-侾丂丂丂亅倱俆倶
丂兤侾丂亖丂倲倎値丂丂丂乮乗乗乗乗乯丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂乮侾俈乯
丂丂丂丂丂丂丂丂丂丂丂丂丂丂倱俆倷
丂偲偟偰丄倱俆偑暘傟偽兤侾偑媮傔傜傟傑偡丅
丂偙偙偱丄恾.侾丄恾.俀傪尒捈偟偰壓偝偄丅
丂慜崁偱傕弎傋傑偟偨偑丄俴俆亖侽偲偟傑偡丅
丂偡傞偲丄俹俆亖俹係偲側傝丄俹俆偑媮傑傟偽俹係傕媮傑傞帠偵側傝傑偡丅
丂埲忋傪摜傑偊偰丄恾.俀傪尒傞偲丄儀僋僩儖倱俆偼儀僋僩儖倢係偲儀僋僩儖倎偺椉曽偵捈岎偡傞儀僋僩儖偱偁傞偙偲偑暘偐傝傑偡丅
丂梫偼懌庱偺曽岦傪帵偡儀僋僩儖偲儀僋僩儖倎偲偵捈岎偡傞扨埵儀僋僩儖偑倱俆乮亖倱係亖倱俁乯偱偁傞偲偄偆偙偲偱偡丅
丂儀僋僩儖倎偼婛抦側偺偱丄懌庱偺曽岦傪昞偡儀僋僩儖傪媮傔傞栿偱偡偑丄懌庱揰俹係偵懳偟偰丄俹侾偺儀僋僩儖暘傪嵎偟堷偗偽丄懌庱偺曽岦偑暘傝傑偡丅乮俹侾偲俹俀偼俴俀亖侽偺堊丄摨偠埵抲偵側傝傑偡乯
丂婡峔忋俹侾偼丄倢侾偲摍壙偱偁傝丄倢侾亖乮侽丄侽丄亅俴侾乯俿偲偟偰兤侾偵娭學柍偔俹侾偼婛抦偲側傝傑偡丅
丂偦偟偰丄俹俆偼俹偵懳偟偰丄儀僋僩儖倎偺媡曽岦偵俴俇乫暘丄儀僋僩儖倐偺媡曽岦俴俇乫乫暘栠偭偨揰偱偡丅
丂儀僋僩儖倎丄倐偼婛抦偱偁傞偺偱丄俹傛傝俹俆偑媮傑傞帠偵側傝傑偡丅
丂埲忋偺帠傪傑偲傔傞偲丄
丂俹俆丂亖丂俹係丂亖丂俹丂亅丂倎俴俇乫丂亅丂倐俴俇乫乫丂丂丂丂丂丂丂丂丂丂丂乮侾俉乯
丂偐傜丄懌庱揰俹係乫偼丄
丂俹係乫丂亖丂俹係丂亅丂俹侾丂亖丂俹丂亅丂倎俴俇乫丂亅丂倐俴俇乫乫丂亅丂俹侾丂丂丂丂丂丂丂丂丂乮侾俋乯
丂傛偭偰丄
丂俹係乫倶丂亖丂俹倶丂亅丂倎倶俴俇乫丂亅丂倐倶俴俇乫乫
丂俹係乫倷丂亖丂俹倷丂亅丂倎倷俴俇乫丂亅丂倐倷俴俇乫乫
丂俹係乫倸丂亖丂俹倸丂亅丂倎倸俴俇乫丂亅丂倐倸俴俇乫乫丂亄丂俴侾
丂扐偟丄偙偺傑傑偱偼俹係乫偼扨埵儀僋僩儖偱偼側偄偺偱丄儀僋僩儖偺挿偝乥俹係乫乥偱妱偭偰傗傞昁梫偑偁傝傑偡丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂2丂丂丂丂丂丂丂2丂丂丂丂丂丂丂2丂丂丂0.5
丂乥俹係乫乥丂亖丂乮俹係乫倶丂丂亄丂俹係乫倷丂丂亄丂俹係乫倸丂丂乯
丂傛偭偰丄俹係乫偺扨埵儀僋僩儖俹係乫乫偼丄
丂俹係乫乫丂亖丂俹係乫乛丂乥俹係乫乥
丂俹係乫乫倶丂亖丂俹係乫倶丂乛丂乥俹係乫乥
丂俹係乫乫倷丂亖丂俹係乫倷丂乛丂乥俹係乫乥
丂俹係乫乫倸丂亖丂俹係乫倸丂乛丂乥俹係乫乥
丂偲側傝傑偡丅
丂偙偺俹係乫乫偲倎偺奜愊傪媮傔傟偽丄捈岎儀僋僩儖偑摼傜傟傑偡丅
丂傑偨丄俹係乫乫丄倎嫟偵扨埵儀僋僩儖偱偁傞偺偱丄奜愊傕帺摦揑偵扨埵儀僋僩儖偲側傝傑偡丅
丂倎丄俹係乫乫偲偺捈岎儀僋僩儖傪倕亖乮倕倶丄倕倷丄倕倸乯俿偲偡傞偲丄
丂倕倶丂亖丂倎倷乮俹係乫乫倸乯丂亅丂倎倸乮俹係乫乫倷乯
丂倕倷丂亖丂倎倸乮俹係乫乫倶乯丂亅丂倎倶乮俹係乫乫倸乯
丂倕倸丂亖丂倎倶乮俹係乫乫倷乯丂亅丂倎倷乮俹係乫乫倶乯
丂扐偟丄忋婰偺媮傔曽偼丄兤俇亖俋侽亱偺帪偵偼惉棫偟側偄偺偱丄懌庱偺壜摦斖埻偼丄亇俋侽亱枹枮偵偡傞昁梫偑偁傝傑偡丅
丂偙傟偱丄
丂倱俆丂亖丂倱係丂亖丂倱俁丂亖丂倕
丂偲側傝丄幃乮侾俈乯傛傝丄
丂丂丂丂丂丂丂丂丂-侾丂丂丂亅倕倶
丂兤侾丂亖丂倲倎値丂丂丂乮乗乗乗乗乯
丂丂丂丂丂丂丂丂丂丂丂丂丂丂倕倷
丂偲摫偐傟傑偡丅
嘦丗兤俀摫弌
丂兤侾偑媮傑傟偽丄斾妑揑娙扨偵媮傔傞偙偲偑弌棃傑偡丅
丂傑偢丄
丂倱俁丂亖丂乮亅俽侾俠俀丄俠侾俠俀丄俽俀乯俿丂亖丂乮倕倶丄倕倷丄倕倸乯俿
丂偱偁傞帠傪棙梡偟偰丄
丂丂丂丂丂丂丂丂丂-侾丂丂丂俽俀丂丂丂丂丂丂丂-侾丂丂丂俽俀
丂兤俀丂亖丂倲倎値丂丂丂乮乗乗乗乯丂亖丂倲倎値丂丂乮乗乗乗乗乗乗乗乗乯
丂丂丂丂丂丂丂丂丂丂丂丂丂丂俠俀丂丂丂丂丂丂丂丂丂丂丂丂俠侾俠俀乛俠侾
丂丂丂丂丂丂丂丂丂-侾丂丂丂倕倸
丂兤俀丂亖丂倲倎値丂丂丂乮乗乗乗乗乯丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂乮俀侽乯
丂丂丂丂丂丂丂丂丂丂丂丂丂倕倷乛俠侾
丂
丂偲媮傔傞帠偑偱偒傑偡丅
嘨丗兤係摫弌
丂兤俁偑愭偠傖側偄偺丠
丂偲巚傢傟傞偐傕偟傟傑偣傫偑丄兤係偺曽偑兤俁傛傝傕摫弌偟傗偡偄偺偱丄偙偪傜偐傜愭偵峴偄傑偡丅
丂傑偢丄恾.俁偺傛偆偵丄懌庱偺曽岦偲埵抲傪帵偡儀僋僩儖俹係乫偺挿偝乥俹係乫乥傪掙曈偲偟丄懠偺擇曈傪俴俁丄俴係乮亖俴俁乯偲偟偨擇摍曈嶰妏宍傪峫偊傑偡丅乮慜弎偟偨俴俁亖俴係偺忦審偼偙偺堊偵愝掕偟偨傕偺偱偡乯
丂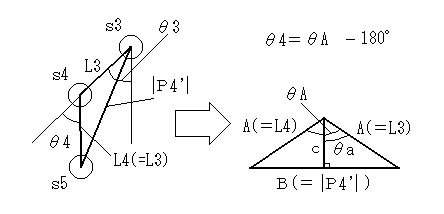
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂恾丏俁
丂偙偺応崌丄倱俁乣倱俆偼暯峴側偨傔丄儀僋僩儖偼忢偵摨偠曽岦偲側傞偨傔丄乥俹係乫乥偺抣偝偊暘傟偽倱俁乣倱俆偺曽岦偼峫偊傞昁梫偼偁傝傑偣傫丅
丂偝偰丄恾.俁偵偍偄偰丄兤A偺妏搙傪媮傔傞偵偼丄
丂俙丒倱倝値乮兤倎乯丂亖丂乮侾乛俀乯丂亊丂俛
丂傛傝丄
丂丂丂丂丂丂丂丂丂-1
丂兤倎丂亖丂倱倝値丂丂丂乮俛乛俀俙乯
丂偙偙偱丄兤倎偼恾.俁偵偍偗傞捈妏嶰妏宍俙俛俠偺妏偺堦偮偱偁傝丄
丂兤俙丂亖丂俀丂亊丂兤倎丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂乮俀侾乯
丂偺娭學偑偁傝傑偡丅
丂嵟廔揑偵丄兤係偼恾.俁偵偁傞捠傝丄
丂兤係丂亖丂兤俙丂亅丂侾俉侽亱
丂偐傜丄
丂丂丂丂丂丂丂丂丂丂丂-1
丂兤係丂亖丂俀乮倱倝値丂丂乮乥俹係乫乥乛俀俴俁乯丂亅丂侾俉侽亱乯丂丂丂丂丂乮俀俀乯
丂偲偟偰媮傔傞帠偑弌棃傑偡丅
嘩丗兤俁摫弌
丂兤係偑媮傑傟偽斾妑揑娙扨偵乧偲偄偆掱妝偱傕柍偄偱偡丅巆擮側偑傜丅
丂傑偢丄俹係偵偮偄偰峫偊偰傒傑偡丅
丂弴塣摦妛夝偐傜丄俹係偼丄
丂丂丂丂丂丂丂乷丂侽丂乸丂丂丂 乷亅俠侾俽俁亅俽侾俽俀俠俁乸丂丂丂丂丂乷亅俠侾俽乮俁亄係乯亅俽侾俽俀俠乮俁亄係乯乸
丂俹係丂亖丂 乷丂侽丂乸丂亄丂乷亅俽侾俽俁亄俠侾俽俀俠俁乸俴俁丂亄丂乷亅俽侾俽乮俁亄係乯亄俠侾俽俀俠乮俁亄係乯乸俴係
丂丂丂丂丂丂丂乷亅俴侾乸丂丂丂乷亅俠俀俠俁丂丂丂丂丂丂丂 乸丂丂丂丂丂 乷亅俠俀俠乮俁亄係乯丂丂丂丂丂丂丂丂丂丂丂 乸
丂偱偁傝丄慜弎偟偨傛偆偵丄俹係亖俹俆偱偁傝丄
丂丂丂丂丂丂丂 乷亅俠侾俽俁亅俽侾俽俀俠俁乸丂丂丂丂丂乷亅俠侾俽乮俁亄係乯亅俽侾俽俀俠乮俁亄係乯乸
丂俹係乫丂亖丂乷亅俽侾俽俁亄俠侾俽俀俠俁乸俴俁丂亄丂乷亅俽侾俽乮俁亄係乯亄俠侾俽俀俠乮俁亄係乯乸俴係
丂丂丂丂丂丂丂 乷亅俠俀俠俁丂丂丂丂丂丂丂 乸丂丂丂丂丂 乷亅俠俀俠乮俁亄係乯丂丂丂丂丂丂丂丂丂丂丂丂乸
丂偲側傝傑偡丅偙偺俹係乫偼愭掱偺俹係乫偺偙偲偱偁傝丄偙偺帪揰偱婛抦偺抣偱偡丅
丂偙偙偐傜丄兤侾丄兤俀偺塭嬁傪彍奜偟傑偡丅
丂嬶懱揑偵偼丄兤侾丄兤俀偺夞揮暘傪彍嫀偟丄婎弨埵抲偵栠偡偙偲偵側傝傑偡丅
丂幃偲偟偰偼丄埲壓偺條偵側傝傑偡丅
丂俹係乫乫乫丂亖丂俤乮亅倝兤俀乯俤乮亅倠兤侾乯俹係乫
丂偙偙偱俤乮亅乣乯偲偄偆偺偼丄偄傢備傞媡峴楍偺偙偲偱丄椺偊偽丂俤乮亅倠兤侾乯俤乮倠兤侾乯亖侾丂偲偄偆惈幙傪帩偪傑偡丅
丂俹係乫偼丄
丂俹係乫丂亖丂俤乮倠兤侾乯俤乮倝兤俀乯俤乮倞兤俁乯倢俁丂亄丂俤乮倠兤侾乯俤乮倝兤俀乯俤乮倞兤俁乯俤乮倞兤係乯倢係
丂偲側傞偺偱丄俹係乫乫乫偼丄
丂俹係乫乫乫丂亖丂俤乮亅倝兤俀乯俤乮亅倠兤侾乯俤乮倠兤侾乯俤乮倝兤俀乯俤乮倞兤俁乯倢俁丂亄丂俤乮亅倝兤俀乯俤乮亅倠兤侾乯俤乮倠兤侾乯俤乮倝兤俀乯俤乮倞兤俁乯俤乮倞兤係乯倢係
丂傛偭偰丄
丂俹係乫乫乫丂亖丂俤乮倞兤俁乯倢俁丂亄丂俤乮倞兤俁乯俤乮倞兤係乯倢係
丂丂丂丂丂丂丂丂丂乷亅俽俁乸丂丂丂丂丂丂乷亅俠俁俽係亅俽俁俠係乸
丂俹係乫乫乫丂亖丂乷丂侽丂丂乸倢俁丂亄丂丂乷丂丂丂丂丂侽丂丂丂丂丂乸倢係
丂丂丂丂丂丂丂丂丂乷亅俠俁乸丂丂丂丂丂丂乷丂俽俁俽係亅俠俁俠係乸
丂偲側傝傑偡丅
丂幚嵺偵偼丄
丂丂丂丂丂丂丂丂丂丂 乷丂丂侾丂丂丂侽丂丂丂丂侽 乸
丂俤乮亅倝兤乯丂亖丂 乷丂丂侽丂丂俠兤丂丂俽兤乸
丂丂丂丂丂丂丂丂丂丂 乷丂丂侽丂亅俽兤丂丂俠兤乸
丂丂丂丂丂丂丂丂丂丂丂乷丂俠兤丂丂俽兤丂 侽乸
丂俤乮亅倠兤乯丂亖丂乷亅俽兤丂丂俠兤丂丂侽乸
丂丂丂丂丂丂丂丂丂丂丂乷丂丂侽丂丂丂侽丂丂丂侾乸
丂傛傝丄
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂乷丂丂俠侾丂丂丂丂俽侾丂丂丂丂丂侽 乸
丂俤乮亅倝兤俀乯俤乮亅倠兤乯丂亖丂 乷亅俽侾俠侾丂丂俠侾俠俀丂丂俽俀乸
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂乷丂俽侾俽俀丂亅俠侾俽俀丂丂俠俀乸
丂偐傜丄
丂丂丂丂丂丂丂丂丂乷丂丂俠侾丂丂丂丂俽侾丂丂丂丂丂侽乸乷俹係倶乫乸
丂俹係乫乫乫丂亖丂乷亅俽侾俠侾丂丂俠侾俠俀丂丂俽俀乸乷俹係倷乫乸丂丂丂丂丂丂丂丂丂丂丂丂丂丂乮俀俁乯
丂丂丂丂丂丂丂丂丂乷丂俽侾俽俀丂亅俠侾俽俀丂丂俠俀乸乷俹係倸乫乸
偙偺曄姺偵傛傝丄俹係乫乫乫偼倷惉暘傪柍偔偟丄倶亅倸暯柺忋偺俀師尦嵗昗宯偱峫偊傞偙偲偑偱偒傞傛偆偵側傝傑偡丅
偙偙偱丄愭偺恾.俁乮嵍恾乯傪尒側偍偡偲丄倷幉懁偐傜尒偨倶亅倸暯柺偺恾偲摍壙偱偁傞偙偲偑暘傝傑偡丅
偦偆偡傞偲丄嘨偱兤係傪媮傔傞嵺偵棙梡偟偨擇摍曈嶰妏宍俙俙俛偺塻妏乮佢俙俛乯偲丄俹係乫乫乫偺妏搙傪崌寁偡傟偽丄兤俁傪摫偗傞偙偲偵側傝傑偡丅
幃偲偟偰偼丄
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂-1丂
丂兤俁丂亖丂佢俙俛丂亄丂倲倎値丂乮亅俹係倸乫乫乫乛俹係倶乫乫乫乯
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂-1
丂兤俁丂亖丂乮俋侽亱丂亅丂兤倎乯丂亄丂倲倎値丂乮亅俹係倸乫乫乫乛俹係倶乫乫乫乯丂丂丂丂丂丂丂丂乮俀係乯
嘪丗兤俆摫弌
丂乧偄偄壛尭偔偳偔側偭偰偒傑偟偨偐丠
丂巹偼傕乕傔偘偦偆偱偡丅
丂偲傝崌偊偢丄兤俆偺摫弌偵偼乮侾俇乯幃傪巊偄傑偡丅
丂丂丂丂丂丂 乷俠侾俠乮俁亄係亄俆乯亅俽侾俽俀俽乮俁亄係亄俆乯乸
丂倱俇丂亖丂乷俽侾俠乮俁亄係亄俆乯亄俠侾俽俀俽乮俁亄係亄俆乯乸丂丂丂丂丂丂丂丂丂丂丂丂丂丂乮侾俇乯
丂丂丂丂丂丂 乷亅俠俀俽乮俁亄係亄俆乯丂丂丂丂丂丂丂丂丂丂丂丂 乸
丂夞揮幉倱俇偺儀僋僩儖偼丄偮傑愭偺曽岦傪帵偡儀僋僩儖倎偲摨偠曽岦傪帵偟傑偡丅
丂偳偪傜傕扨埵儀僋僩儖偱偁傝丄
丂倎丂亖丂倱俇
丂偲偄偆偙偲偵側傝傑偡丅
丂偝偰丄幃乮侾俇乯傛傝丄倱俇倸偵拲栚偟傑偡丅
丂倱俇倸丂亖丂倎倸丂亖丂亅俠俀俽乮俁亄係亄俆乯
丂亅倎倸乛俠俀丂亖丂俽乮俁亄係亄俆乯
丂傛傝丄
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂-1
丂兤俁丂亄丂兤係丂亄丂兤俆丂亖丂倱倝値丂乮亅倎倸乛俠俀乯
丂丂丂丂丂丂丂丂丂-1
丂兤俆丂亖丂倱倝値丂乮亅倎倸乛俠俀乯丂亅丂兤俁丂亅兤係丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂乮俀俆乯
丂偲側傝丄兤俆傪摫弌偱偒傑偡丅
嘫丗兤俇摫弌
丂傗偭偲杮復嵟屻偱偡丅
丂婃挘傝傑偟傚偆丅乮傓偟傠帺暘偵尵偄暦偐偣乯
丂兤俇傪摫弌偡傞偺偵巊梡偡傞偺偼幃乮侾侽乯偱偡丅
丂丂丂丂丂丂乷亅俠侾俽乮俁亄係亄俆乯俠俇亅俽侾俠俀俽俇亅俽侾俽俀俠乮俁亄係亄俆乯俠俇乸
丂倐丂亖丂 乷亅俽侾俽乮俁亄係亄俆乯俠俇亄俠侾俠俀俽俇亄俠侾俽俀俠乮俁亄係亄俆乯俠俇乸丂丂丂丂丂丂丂丂丂丂乮侾侽乯
丂丂丂丂丂丂乷俽俀俽俇亅俠俀俠乮俁亄係亄俆乯俠俇丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 乸
丂偦偺傑傫傑倐傪昞偟偰偄傞偺偱丄婛抦偱偁傞倐偲丄偙傟傑偱媮傔偰棃偨兤侾乣兤俆傪梡偄傟偽媮傔傞偙偲偑偱偒傑偡丅
丂傑偢丄
丂俠侾倐倶丂亄丂俽侾倐倷丂亖丂亅俽乮俁亄係亄俆乯俠俇
丂偲偱偒傞偺偱丄
丂亅乮俠侾倐倶丂亄丂俽侾倐倷乯乛俽乮俁亄係亄俆乯丂亖丂俠俇
丂傛傝丄
丂丂丂丂丂丂丂丂丂-1
丂兤俇丂亖丂們倧倱丂乮亅乮俠侾倐倶丂亄丂俽侾倐倷乯乛俽乮俁亄係亄俆乯乯
丂偙傟偱丄兤侾乣兤俇偑慡偰媮傑傝傑偟偨丅
丂嵟廔揑偵偼丄廳怱偵壛傢傞儌乕儊儞僩傗巔惃傪峫椂偟偨忋偱丄懌偵栚昗抣傪梌偊傞栿偱丄偙傟偱廔椆偲偄偆帠偼柍偔丄応崌偵傛偭偰偼慡恎偵偮偄偰偺媡塣摦妛傪夝偔昁梫偑惗偠傞偐傕偟傟傑偣傫偑丄弴塣摦妛丄媡塣摦妛偺夝偺峫偊曽帺懱偼崱夞偱恎偵晅偄偨偲峫偊傑偡丅
丂廳怱偵偮偄偰傕丄弴塣摦妛傪墳梡偡傞偙偲偱嶼弌壜擻偲巚傢傟傑偡丅
丂乧崱夞偼摫弌偟偰傑偣傫偑丅乮丱丱丟
丂
丂
丂栠傞
丂
丂
丂
丂

