財務関数理解のために

【１：用語】

◎借方・貸方

借方

貸方
資産を増加させる科目 資産を減少させる科目
負債を減少させる科目 負債を増加させる科目
資本を減少させる科目 資本を増加させる科目
費用を発生させる科目 収益を発生させる科目

例1)現金で \10,000 の備品を購入したとき
 

借方

貸方

  
備品という資産の増加→ 備品 \10,000 現金 \10,000 ←現金という資産の減少

例2)\10,000の商品を販売し現金で入金したとき
 

借方

貸方

  
現金という資産の増加→ 現金 \10,000 売上 \10,000 ←収益の発生

◎Ｂ／Ｓ
貸借対照表

◎Ｐ／Ｌ
損益計算書

◎利息計算の方法
残債方式
　前回の返済後の借入残高に利率を掛けて支払利息を計算する。
　借入金の返済が進んでいくにしたがって支払利息が減少する。
アドオン方式
　当初の借入金額を元に支払利息を計算する。

◎返済方式
元金均等返済
　　毎回の借入金元本の返済額が一定。
　　元本の返済額に利息を足したものが毎回の支払額となる。
　　返済が進んでいくと支払利息金額は減少していく。
元利均等返済
　　元本と利息の支払合計が毎回一定となる。
　　利息計算の方式がアドオン方式ならば毎回の支払額に占める元本と利息の割合が一定となる。
　　利息計算の方式が残債方式ならば毎回の支払額に占める元本と利息の割合は変化していく。
　　一般に元利均等返済方式という場合には残債方式によって利息計算をする。

◎複利計算
元本に利息を繰り入れて次の期の元本とするやりかた。

◎キャッシュフロー
金の流れ。
出ていく金(支払い)ならマイナス。入ってくる金(受け取り)ならプラス。

◎現在価値(割引現価)
一定期間にわたって投資される資本の現時点での価値。 
　　例) \100,000 を年利 10% で運用したとき
　　　　　１年後 ………………………………………… \100,000 * 1.1 = \110,000
　　　　　１年後の \100,000 は 現在のいくらか？… \100,000 / 1.1 =  \90,909

◎正味現在価値
現在の投資額と将来のキャッシュフローの現在価値の総和の差

◎内部利益率(ディスカウント・キャッシュフロー)
現在の投資額と将来のキャッシュフローの現在価値の総和が等しくなるような利率

◎投資に関する各項目の関係式
( 現在価値 * (1+利率)^期間 )+( 定期支払額 * (1+利率*(期末or期首) ) * ( ((1+利率)^期間 -1) / 利率 ) + 将来価値 = 0
　　※期末の場合は「1」、期首の場合は「0」とする。

【２：現在価値の考え方】

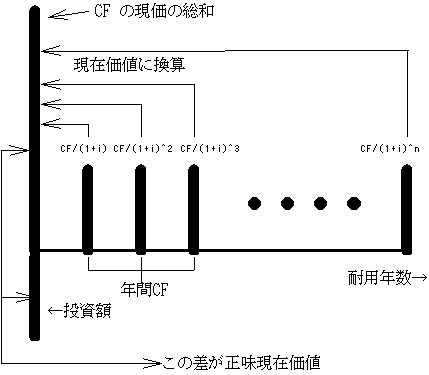
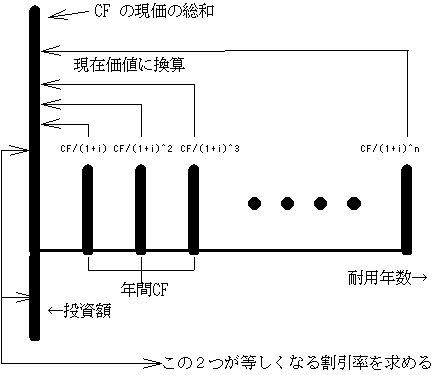
※ CF ・・・キャッシュフロー
       CF/(1+i)+CF/(1+i)2+CF/(1+i)3 ・・・ +CF/(1+)n=(((1+i)n-1/i(1+i)n)*CF
年金原価係数

＜年金原価係数表＞
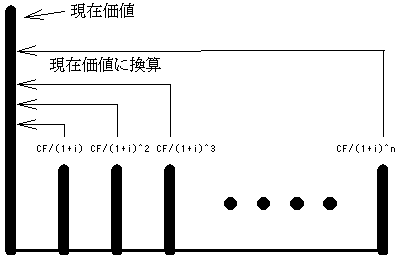
  利率                
年 10% 11% 12% 13% 14% 15% 16% 17% 18%
1 0.909 0.901 0.893 0.885 0.877 0.870 0.862 0.855 0.847
2 1.736 1.713 1.690 1.668 1.647 1.626 1.605 1.585 1.566
3 2.487 2.444 2.402 2.361 2.322 2.283 2.246 2.210 2.174
4 3.170 3.102 3.037 2.974 2.914 2.855 2.798 2.743 2.690
5 3.791 3.696 3.605 3.517 3.433 3.352 3.274 3.199 3.127
6 4.355 4.231 4.111 3.998 3.889 3.784 3.685 3.589 3.498
7 4.868 4.712 4.564 4.423 4.288 4.160 4.039 3.922 3.812
8 5.335 5.146 4.968 4.799 4.639 4.487 4.344 4.207 4.078
9 5.759 5.537 5.328 5.132 4.946 4.772 4.607 4.451 4.303
10 6.145 5.889 5.650 5.426 5.216 5.019 4.833 4.659 4.494

【３：現在価値法の主要項目】

＜正味現在価値法＞
正味現在価値＝CF の原価の総和−投資額>

＜内部利益率（ディスカウント・キャッシュフロー）法＞
CF の現価の総和＝投資額 となるような割引率

【４：ローン計算】

引数 
   利率　　　利率(年利) > -1
   返済期間　何番目の単位期間か
   期数　　　返済期間(年)
   借入金額　借入元金
   将来価値　投資のある時点での価値
   タイプ　　返済(キャッシュフロー)がいつ行われるかのフラグ
   　　　　　ex)月末 = 0　月初 = 1
                期        利息計算をしたい n 番目の期
   ※月単位の値を求める場合は  利率/12  期数*12  として引数を指定する。
@IPAYMT(利率, 返済期間, 期数, 借入金額 <,将来価値> <,タイプ>)
返済期間(1〜期数)で指定された時点での残存元金に対する利息
ローン返済の場合は完済されるので将来価値は 0 となる

@PPAYMT(利率, 返済期間, 期数, 借入金額 <,将来価値> <,タイプ>)
返済期間(1〜期数)で指定された時点での残存元金
ローン返済の場合は完済されるので将来価値は 0 となる

@PAYMT(利率, 期数, 借入金額 <,将来価値> <,タイプ>)
元利均等返済額(期首返済 or 期末返済選択可)
ローン返済の場合は完済されるので将来価値は 0 となる

@PMT(借入金額, 利率, 期数 <,タイプ>)
元利均等返済額(期首返済 or 期末返済選択可)

@PMT2(借入金額, 利率, 期数)
元利均等返済額(期首返済固定)

@GANKIN(借入金額, 利率, 期数,期)、@SPI(借入金額, 利率, 期数,期)
元金均等返済方式の場合の、期(1〜期数)で指定された時点での利息

@GANRI(借入金額, 利率, 期数, 期)、@PMTI(借入金額, 利率, 期数, 期)
元利均等(残債)方式の場合の、期(1〜期数)で指定された時点での利息

【５：投資計算】

引数 
  利率      利率(年利) > -1
  返済期間  何番目の単位期間か
  期数      返済期間(年)
  借入金額  借入元金
  将来価値  投資のある時点での価値
  タイプ    返済(キャッシュフロー)がいつ行われるかのフラグ
            ex)月末 = 0   月初 = 1
  期        利息計算をしたい n 番目の期
  ※月単位の値を求める場合は  利率/12  期数*12  として引数を指定する。
@NPV(利率, 範囲 <,タイプ>)
投資の現在価値(キャッシュフローが一定でない場合も可)

@PV(投資額, 利率, 期数 <,タイプ>)
キャッシュフローが一定の場合の投資の現在価値

@PV2(投資額, 利率, 期数)
キャッシュフローが一定の場合の投資の現在価値(期首払固定)

@PVAL(利率, 期数, 投資額 <,将来価値> <,タイプ>)
投資額を指定し将来価値を 0 とすると、期数年間の年金受け取り総額の現在価値
投資額を 0 とし将来価値を指定すると、期数年後の一括受け取り金額の現在価値

@FV(投資額, 利率, 期数 <,タイプ>)
一定の額で積み立て投資したときの将来価値(=満期額)

@FV2(投資額, 利率, 期数)
一定の額で積み立て投資したときの将来価値(=満期額)
ただし積み立ては期首固定

@FVAL(利率, 期数, 投資額 <,現在価値> <,タイプ>)
一定の額で積み立て投資したときの将来価値(=満期額)
頭金の金額を現在価値として指定可能

@TERM(投資額, 利率, 満期額 <,タイプ>)
定期積み立ての時の満期額までの期間数

@TERM2(投資額, 利率, 満期額)
定期積み立ての時の満期額までの期間数
ただし積み立ては期首固定

@CTERM(利率, 満期額, 元金)
元金が満期額になるまでの期間数

@NPER(利率, 投資額, 元金, 満期額 <,タイプ>)
一定の額で積み立て投資したときの満期額までの期間数
頭金の金額を元金として指定可能

@IRATE(期数, 投資額, 現在価値 <,将来価値> <,タイプ>)
元金(現在価値)に加えて、期数間一定の積み立て(投資額)をしたときの満期額(将来価値)に到達するための利率

@RATE(将来価値, 現在価値, 期数)
元金(現在価値)を期数間運用したときの満期額(将来価値)に到達するための利率

@IRR(推定利益率, 範囲)
投資の内部利益率
投資の現在価値( @PV の計算結果 )が 0 となるような利率

【６：減価償却】

引数 
     取得原価  資産の購入価格
     残存値額  耐用年数が終了したときの資産の残存価値
     耐用年数  法令で定められた耐用年数
     使用年数  資産を使用した年数
@DB(取得原価, 残存値額, 耐用年数, 使用年数)
定率法減価償却額
　償却額 = (1 - (残存値額/取得原価)^(1/耐用年数)) * 前期末の未償却残高
　日本の税法では償却率を小数点以下４位で四捨五入するため、@DB関数の計算結果をそのまま使うことができない。
　税法上の償却率 = @ROUND(@DB(1, 0.1, 耐用年数, 1), 3)
　税法上の償却額 = @INT(取得原価 * 償却率)

@DDB(取得原価, 残存値額, 耐用年数, 使用年数)
倍定率(倍率)法減価償却額
　償却額 = (取得原価 - 累積償却額)*2 / 耐用年数
　日本の税法では認められていない。

@SYD(取得原価, 残存値額, 耐用年数, 使用年数)
算術級数(定額逓減)法減価償却額
　償却額 = (取得原価-残存値額)*(耐用年数-使用年数+1) / 耐用年数(耐用年数+1)/2
　日本の税法では認められていない。

@SLN(取得原価, 残存値額, 耐用年数)
　定額法減価償却額
　償却額 = (取得原価-残存値額)/耐用年数
　日本の税法では償却率を小数点以下４位で四捨五入するため、@SLN関数の計算結果をそのまま使うことができない。
　税法上の償却率 = @INT( @SLN(取得原価, 残存値額, 耐用年数)/10 ) / 1000
　税法上の償却額 = @INT(取得原価 - 残存値額) * 償却率