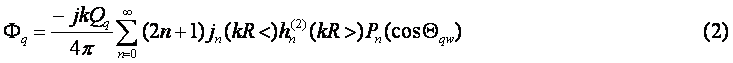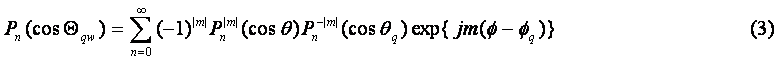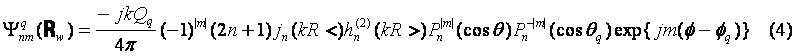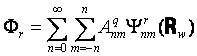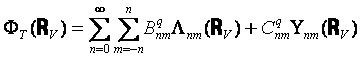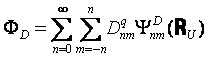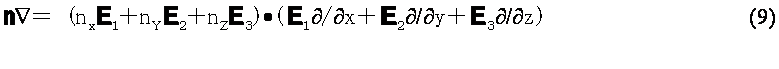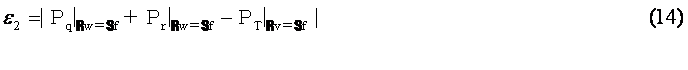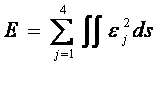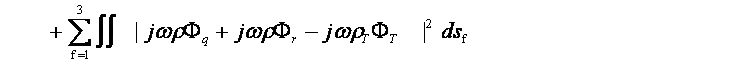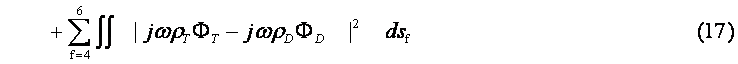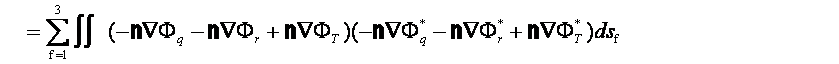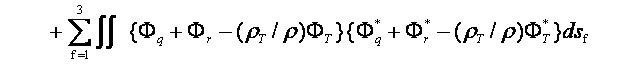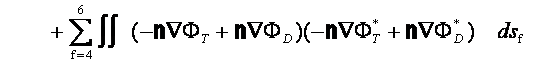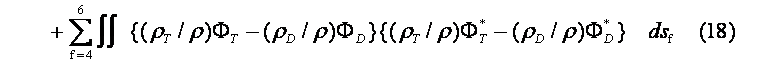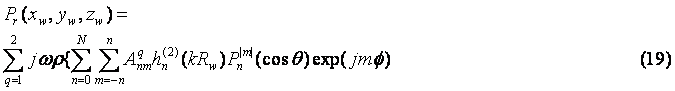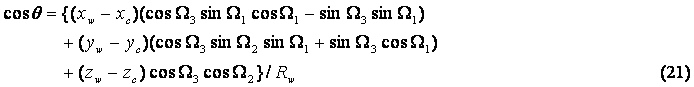|
—LŒہ’·’eگ«‰~“›‚ة‚و‚éژU—گ‰¹ڈê‚جŒں“¢
|
|
||
|
‚PپD‚ح‚¶‚ك‚ة ٹC—mٹد‘ھ‚âٹC’ê’Tچ¸‚إ—p‚¢‚ç‚ê‚鉹Œ¹‚ئ‚µ‚ؤپCˆہ’è‚ة‘هƒpƒڈپ[‚ً”گ¶‚إ‚«‘—گMڈî•ٌ‚ًƒRƒ“ƒgƒچپ[ƒ‹‚إ‚«‚é–ûˆ³گ§Œنژ®’لژü”g‰¹Œ¹‚جٹْ‘ز‚ھچ‚‚ـ‚ء‚ؤ‚¢‚éپB‚µ‚©‚µٹY‰¹Œ¹‚ح,‚±‚¤‚µ‚½—ک“_‚ة”½‚µژہچغٹC—m‚âٹC’ê‚ة•~گف‚ ‚é‚¢‚ح‰gچq‘ج‚ب‚ا‚ة‘•”ُ‚µ‚ؤŒ،ˆّ‚·‚é‚ئ‚ب‚é‚ئ”ٌڈي‚ة‘هٹ|‚©‚è‚ب‚à‚ج‚ئ‚ب‚éپB‚»‚ê‚ح‰¹Œ¹ژ©‘ج‚ھ‘هƒpƒڈپ[‚ً”گ¶‚·‚邽‚ك•K‘R“I‚ة‘ه‚«‚‚ب‚é‚ج‚ة‰ء‚¦,گأگ…ˆ³‚ج‘ه‚«‚¢گ[پX |
|
||
|
|
“x‚إ‰^—p‚³‚ê‚é‚ج‚إ‘—”gگU“®”آ‘OŒم‚ج‹دˆ³•âڈ‘•’u‚ھ•K—v‚ئ‚ب‚邽‚ك‚إ‚ ‚éپB‹دˆ³•âڈ‘•’u‚ة‚حˆ³ڈkƒKƒX‚ً••“ü‚µ‚½—eٹي‚ھژg‚ي‚ê‚éپB‚±‚ج—eٹي‚ھŒ‹چ\‘ه‚«‚¢پB‚ـ‚½–ûˆ³ƒRƒ“ƒgƒچپ[ƒ‹—p–û’™‚ك—eٹي‚ب‚ا‚ج‘•’u‚à•K—v‚ئ‚ب‚éپB‚±‚ê‚ç‚ً•âڈ—p—¬‘ج—eٹي‚ئŒؤ‚شپiگ}1‚ة•âڈ—p—¬‘ج—eٹي‚ًژ¦‚·پjپB‚±‚ج‚و‚¤‚ة‚µ‚ؤ‘•”ُ‚ھ‘هٹ|‚©‚è‚ة‚ب‚é‚ج‚إƒRƒXƒg“I‚ب‰ü‘P‚ھ–]‚ـ‚ê‚éپB‘هٹ|‚©‚è‚ة‚ب‚é‚ج‚ح,”ً‚¯‚ç‚ê‚ب‚¢‚ئ‚µ‚ؤ,‚½‚¾‚±‚±‚إˆê”شڈd—v‚ة‚ب‚ء‚ؤ‚‚é‚ج‚ھ‰¹‹؟گ«”\‚إ‚ ‚éپB•âڈ—p—¬‘ج—eٹي‚ھ‰“‹——£‚ة’u‚©‚ꂽ‚ئ‚«‰¹Œ¹گ«”\‚ة–â‘è‚ح–³‚¢پB‚ئ‚±‚ë‚ھپC•âڈ—eٹي‚ًژہ‘•ڈم‚إ‚«‚邾‚¯ƒRƒ“ƒpƒNƒg‚ة‚·‚邽‚ك‰¹Œ¹’P‘ج•t‹ك‚ة‚¨‚‚ئ,‚±‚ج•âڈ—eٹي‚©‚特”g”½ژث‚ھ”گ¶‚·‚éپB‰¹Œ¹’P‘ج‚إ‚ح–³ژwŒüگ«‚إ‘ه‰¹ˆ³‚ً”گ¶‚إ‚«‚ؤ‚àپC—eٹي‚ج”½ژث‚ة‚و‚èƒ_ƒ“ƒsƒ“ƒO‚³‚ꂽ‚è,‚ ‚é‚¢‚ح‰¹Œ¹‚ةژwŒüگ«‚ھ•t‚¯‚ç‚ê‚é‚و‚¤‚ة‚ب‚ء‚ؤ‚حچD‚ـ‚µ‚‚ب‚¢پB |
|
|
|
گ}1پ@•âڈ—p—¬‘ج—eٹي |
|
||
|
‚±‚±‚إ‚ح,‚±‚ج—eٹي‚ة‚و‚鉹”g”½ژث‚جŒں“¢‚ًچs‚¤پB—eٹي‚حگ}1‚ج‚و‚¤‚ب‰~“›—eٹي‚ھˆê”ت‚ة‚و‚ژg‚ي‚ê‚éپB‚»‚±‚إ‰~“›ڈَ‚ج‹à‘®—eٹي‚ًژو‚èڈم‚°‚邱‚ئ‚ة‚µپC—eٹي“à•”‚ة‰t‘ج‚â‹َ‹C‚ًڈ[“U‚·‚郂ƒfƒ‹‚إ”½ژث‚جŒں“¢‚ًچs‚¤پB‚ئ‚±‚ë‚إ—eٹي“™‚ة‚و‚锽ژث‰ًگحƒ‚ƒfƒ‹‚ئ‚µ‚ؤ,‚و‚‹…‚â‰ٌ“]‘ب‰~‘ج‚â–³Œہ’·‰~’Œ‚جƒ‚ƒfƒ‹‚ً—p‚¢‚½‰ًگح‚ھ‚ب‚³‚ê‚ؤ‚¢‚é1پjپ|3پjپB‚ـ‚½‹ك”NStanton4پj‚ح,ٹب’P‚ب‹كژ—“Iژè–@‚ً—p‚¢‰~“›’·‚³پ^‰~“›ٹOŒa‚ج”ن‚ج’l‚ھ‘ه‚«‚¢—LŒہ’·‰~’Œ‚ة‚آ‚¢‚ؤ,‰~“›ژ²‚ةگ‚’¼“üژث‚·‚鉹”g‚ة‚و‚éƒ^پ[ƒQƒbƒgƒXƒgƒŒƒ“ƒOƒXپiٹب’P‚ةŒ¾‚¦‚خ,‰~“›—eٹي‚ض‚ج“üژث”g‚ة‘خ‚·‚锽ژث”g‚ج‹‚³‚جٹ„چ‡‚ة‘ٹ“–پj‚ً‹پ‚ك”½ژث‰ًگح‚ً‚µ‚ؤ‚¢‚éپB‚µ‚©‚µ,Œ»ژہ“I‚ب‰~“›—eٹي‚ة‘خ‚µ‹ك‹——£‚إ‚»‚جŒX‚«‚ً•د‚¦‚½ڈêچ‡‚ة‚آ‚¢‚ؤ”½ژث‰ًگح‚ً‚µ‚½—ل‚ح‚ ‚ـ‚è–³‚¢‚و‚¤‚إ‚ ‚éپB •Mژز‚حگو‚ة,’eگ«‰~“›ٹk‚ج—¼’[–ت‚ة‘—”gگU“®”آ‚ًژو‚è•t‚¯‚½‰¹Œ¹‚ج”گ¶‚·‚鉹ڈê‰ًگح‚ًچs‚ء‚½پB‰~“›‘¤–ت‚ة“§‰ك‚·‚é‰ٌگـ”g,‚¨‚و‚ر‰~“›“à•”‚©‚ç”گ¶‚·‚锽ژث”g‚ً‘S‚ؤچl—¶‚µ‚½‰¹ڈêŒvژZ–@پielasticپ@modeپ@analysis5پj‚ئŒؤ‚شپj‚ة‚و‚é‰ًگح‚إ‚ ‚éپBژہچغ‚ة‚±‚جŒvژZ–@‚إ,گ»چى‚µ‚½‰~“›‰¹Œ¹‚ھپCگ…‘…“à‚إ”گ¶‚·‚鉹ڈê‚ًŒvژZ‚µژہŒ±’l‚ئ”نٹr‚µ‚½‚ئ‚±‚ë,‹ة‚ك‚ؤ‹ك‚¢’l‚ج“¾‚ç‚ê‚邱‚ئ‚ھ”»‚ء‚½پB‚»‚µ‚ؤ‰¹Œ¹گ،–@‚جچإ“KŒں“¢‚ض‚ئ”“W‚³‚¹,(‚P)‰~“›‚جٹO”¼Œa‚ئ“÷Œْ‚ً•د‚¦‚½ڈêچ‡‚Uپj‚ئ,پi‚Qپj‰~“›â‘جچ‚‚³‚ئ“÷Œْ‚ً•د‚¦‚½ڈêچ‡‚Vپj‚ج”گ¶‰¹ˆ³‚ج‘Œ¸‚ً—\‘ھ‚µ‚½پB پ@elasticپ@modeپ@analysisپ@‚حپC‰¹Œ¹‚ةŒہ‚炸‰¹”gژU—گ‘ج‚ئ‚ب‚é‰~“›ٹk‚جژU—گ‰ًگح‚ة‚à‰—p‚إ‚«‚é‚ئژv‚ي‚ê‚éپB‚»‚±‚إپC‚±‚جelasticپ@modeپ@analysis‚ج‰~“›—eٹي‚جژU—گ‰ًگح‚ض‚ج“K—p‚ًژژ‚ف‚éپB‹«ٹEڈًŒڈ‚ج—^‚¦•û‚ح‰¹Œ¹’P‘ج‚ج‰ًگح‚ئ“¯‚¶‚إ‚ ‚é‚ھپC‰¹Œ¹‚جˆت’u‚ئژU—گ‘ج‚©‚ç”گ¶‚·‚éژU—گ”g‚ج‰¹Œ¹’†گS‚جˆت’u‚ھ‚¸‚ê‚邽‚كگV‚½‚بژU—گ‰¹ڈê‚ج’èژ®‰»‚ھ•K—v‚ئ‚ب‚éپBژn‚ك‚ة‹ك‹——£ڈê‚إ”Cˆس‚ة’u‚©‚ꂽ—LŒہ’·‰~“›‚ة‚و‚éژU—گ‰¹ڈê‚ً’èژ®‰»‚·‚éپB‚»‚µ‚ؤ’èژ®‰»‚µ‚½ژU—گ‰¹ڈê‚ً—p‚¢‚ؤگ”’lŒvژZ‚ًچs‚¤پB‚±‚±‚إ‚ح,‰~“›“à”}ژ؟‚ًگ…‚ـ‚½‚ح‹َ‹C‚ئ‚µ,‰~“›—eٹي“÷Œْ‚ً•د‚¦‚½ڈêچ‡‚جƒ^پ[ƒQƒbƒgƒXƒgƒŒƒ“ƒOƒXپi’P‚ة‚s‚r‚ئ•\‹L‚·‚éپj‚ً‹پ‚ك‰~“›—eٹي‚ج”½ژث‚ًŒں“¢‚·‚éپB‚ـ‚½•tک^‚ة,Stanton‚ة‚و‚ء‚ؤ’ٌˆؤ‚³‚ê‚ؤ‚¢‚é‚s‚rŒvژZژ®‚ة‚و‚錋‰ت‚ئelasticپ@modeپ@analysis‚جŒvژZŒ‹‰ت‚ً”نٹr‚µŒں“¢‚·‚éپB |
|
||
|
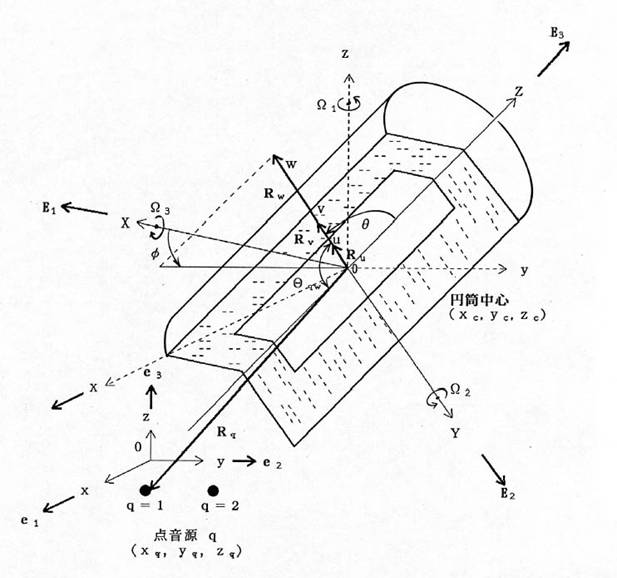
‚QپD—ک_‰ًگح ‚QپD‚P‰¹ڈê‚ج’èژ®‰» –{‰ًگح‚ة‚¨‚¢‚ؤ,—LŒہ’·‰~“›پiˆبŒم’P‚ة‰~“›‚ئŒؤ‚شپj‚ج•دŒ`‚ح,’لژü”g‚ً‘خڈغ‚ئ‚µ’eگ«”g‚ج‚¤‚؟‰¹”gپi‘e–§”gپj‚ج‚ف‚ة‚و‚é•دŒ`‚ًژو‚舵‚¤پB‰¹Œ¹‚حپC‰~“›Œ^‚إ‰~“›Œ^â‘ج‚ج—¼’[–ت‚ة‰~”آڈَƒsƒXƒgƒ“گU“®”آپi‘—”g–تپj‚ً—L‚·‚é‚ھپC‚±‚±‚إ‚ح‘—”g–ت‚ج”}ژ؟”rڈœ‘¬“x‚ئ“¯ˆê‚ج”}ژ؟”rڈœ‘¬“x‚ًژ‚ء‚½“_‰¹Œ¹‚ً‘—”g–ت‚ة’u‚¢‚ؤ‹كژ—‚·‚é،‚·‚ب‚ي‚؟â‘ج‚ًچl‚¦‚ب‚¢‚إ“ٌ“_‰¹Œ¹‚إ‰¹Œ¹‚ً‹كژ—‚·‚é،â‘ج‚ھچ„‚إ‚»‚جگ،–@‚ھ‘—”gژü”gگ”‚ج”g’·‚ة”ن‚ׂؤ‹ة‚ك‚ؤڈ¬‚³‚¢‚ب‚ç‚خپC‚±‚ج‹كژ—‚ح‘أ“–‚إ‚ ‚é‚Wپj، پ@پ@گ}‚Q‚ة‰ًگحƒ‚ƒfƒ‹‚ئ‚µ‚ؤ–³Œہ‚جگ…’†‚ة’u‚©‚ꂽ“_‰¹Œ¹‚ئ“à•”‚ة”}ژ؟‚ً—L‚·‚é‰~“›‚ًژ¦‚·پB’¼Œًگâ‘خچہ•W‚ًگ}‚ج‚و‚¤‚ةپi‚کپC‚™پC‚ڑپj‚إ’è‹`‚·‚é،‚³‚ç‚ةپi‚ک‚ƒپC‚™‚ƒپC‚ڑ‚ƒپj‚ةŒ´“_‚ًˆع“®‚µŒ´“_ژü‚è‚ة‰ٌ“]‚µ‚½’¼Œً‘ٹ‘خچہ•Wپi‚w,‚x,‚yپj‚ًچl‚¦‚éپB‚±‚ج’¼Œً‘ٹ‘خچہ•Wڈم‚ة’†گS‚ھپi‚ک‚ƒپC‚™‚ƒپC‚ڑ‚ƒپjپC’†گSژ²‚ھ‚yژ²‚ئˆê’v‚·‚é‚و‚¤‚ة‰~“›پi‰¹”gژU—گ‘ج‚ئ‚µ‚ؤ‚ج‰~“›پj‚ً’u‚پB‚±‚ج‰~“›‚حٹO”¼Œa‚پ,چ‚‚³‚ˆ‚ئ‚·‚éپB‚±‚±‚إ’¼Œً‘ٹ‘خچہ•Wپi‚w,‚x,‚yپj‚ح,چإڈ‰‚wژ²,‚xژ²,‚yژ²‚ھ‚»‚ꂼ‚êxژ²,yژ²,zژ²‚ئ“¯ˆê•ûŒü‚ئ‚ب‚é‚و‚¤‚ة‘I‚ر,گو‚¸‚yژ²‚ً‚ڑژ²ژü‚è‚ةƒ¶1‰ٌ“]‚µ,‚xژ²ژü‚è‚ةƒ¶2‰ٌ“]‚µ,‚wژ²ژü‚è‚ةƒ¶3‰ٌ“]‚µ‚ؤگف’肳‚ê‚é‚à‚ج‚ئ‚·‚éپB چX‚ة‰~“›’†گS‚©‚çگ…’†”Cˆس‚ج“_‚—‚ًŒ‹‚شƒxƒNƒgƒ‹‚ً‚q‚v‚ئ‚µپC‰~“›’†گS‚ئ‚—‚ًŒ‹‚شگü•ھڈم‚إ‰~“›•ا•”‚ج”Cˆس‚ج“_‚–‚ًŒ‹‚شƒxƒNƒgƒ‹‚ً‚q‚uپC‰~“›“à”}ژ؟‚ج”Cˆس‚ج“_‚ًŒ‹‚شƒxƒNƒgƒ‹‚ً‚q‚t‚ئ‚·‚é،‚q‚vپC‚q‚uپC‚q‚t‚ً‘ٹ‘خ‹ةچہ•W‚إ‚»‚ꂼ‚êپi‚q‚vپCƒئپCƒسپjپCپi‚q‚uپCƒئپCƒسپjپCپi‚q‚tپCƒئپCƒسپj‚ئ’è‹`‚µپC‘ٹ‘خ‰~’Œچہ•W‚إپi‚’‚vپC‚ڑ‚vپCƒسپjپCپi‚’‚uپC‚ڑ‚uپCƒسپjپCپi‚’‚tپC‚ڑ‚tپCƒسپj‚ئ’è‹`‚·‚é،‚ـ‚½گ}‚ج‚و‚¤‚ة“_‰¹Œ¹‚‘‚جˆت’u‚ًپi‚ک‚‘پC‚™‚‘پC‚ڑ‚‘پjپCپi’A‚µ‚‘=1پC2پj‚ئ‚·‚é،Œ´“_‚ئ‚‘‚ًŒ‹‚شƒxƒNƒgƒ‹‚ً‚q‚‘‚ئ‚·‚é،‚q‚‘‚ً‹ةچہ•WŒn‚إپi‚q‚‘پCƒئ‚‘پCƒس‚‘پjپC‰~’Œچہ•WŒn‚إپi‚’‚‘پC‚ڑ‚‘پCƒس‚‘پj‚ئ’è‹`‚·‚é،‚ـ‚½‚q‚‘‚ئ‚q‚v‚ج‚ب‚·ٹp‚ًƒ¦‚‘‚v‚ئ‚·‚é،گâ‘خچہ•W‚ج‚ک•ûŒüپC‚™•ûŒüپC‚ڑ•ûŒü‚ج’PˆتƒxƒNƒgƒ‹‚ً‚»‚ꂼ‚ê‚…1پC‚…2پC‚…3پCگâ‘خچہ•W‚ج‚w•ûŒüپC‚x•ûŒüپC‚y•ûŒü‚ج’PˆتƒxƒNƒgƒ‹‚ًپC‚»‚ꂼ‚ê‚d1پC‚d2پC‚d3‚ئ’è‹`‚·‚é،
|
|
||
|
|
|
||
|
گ}‚Qپ@–³Œہ‚جگ…’†‚ج’u‚©‚ꂽ“_‰¹Œ¹‚ئ“à•”‚ة”}ژ؟‚ً—L‚·‚é‰~“› |
|
||
|
“_‰¹Œ¹‚‘‚©‚çژثڈo‚³‚ꂽ”}ژ؟”rڈœ‘¬“x‚p‚‘‚ج‹…–ت”g‚ھ”}ژ؟’†”Cˆس‚ج“_‚—‚ة”گ¶‚·‚鑬“xƒ|ƒeƒ“ƒVƒƒƒ‹ƒ³‚‘‚حپC
‚ئ•\‚³‚ê‚éپB‚½‚¾‚µپC‚‹‚حگ…‚ج”gگ”ƒض/C,پiƒضپFٹpژü”gگ”پCC:گ…‚ج‰¹‘¬پjپC‚±‚±‚إ‚حژٹش‚جٹضگ”‚…xp(‚ٹƒض‚”)‚ًڈب—ھ‚·‚éپB |
|
||
|
–”پCژ®پi1پj‚ح–³Œہ‰“‚إ•ْژثڈًŒڈ‚ً–‘«‚·‚é‚ج‚إپC‹ةچہ•W‚ً—p‚¢‚½‹‰گ”“WٹJ‚إپC پ@پ@پ@پ@
‚ج‚و‚¤‚ة•\‚³‚ê‚é‚Xپj،’A‚µپC‚ٹ‚ژپCh‚ژپi‚QپjپCP‚ژ‚ح‚ژژں‚ج‚»‚ꂼ‚ê‘وˆêژي‹…ƒxƒbƒZƒ‹ٹضگ”پC‘و“ٌژي‹…ƒnƒ“ƒPƒ‹ٹضگ”پC‘وˆêژيƒ‹ƒWƒƒƒ“ƒhƒ‹ٹضگ”پCRپƒ:minپiR‚vپCR‚‘پjپCRپ„پFmaxپiR‚vپCR‚‘پj‚إ‚ ‚é،ژ®پi‚Qپj’†پCP‚ژ(cosƒ¦‚‘‚v)‚ًƒ‹ƒWƒƒƒ“ƒhƒ‹‚ج”†ٹضگ”‚ج‰ء–@’è—‚P‚Oپj‚ً—p‚¢‚ؤپC
’A‚µپC
‚ب‚éٹضŒWژ®‚ھ“¾‚ç‚ê‚é، پ@ˆê•ûپCژU—گ”g‚ھ“_w‚ة”گ¶‚·‚鑬“xƒ|ƒeƒ“ƒVƒƒƒ‹‚ًƒ³r‚ئ‚·‚é‚ئپC–³Œہ‰“‚إ•ْژثڈًŒڈ‚ً–‘«‚·‚é‚ج‚إ‹‰گ”“WٹJ‚إپCپ@پ@
’A‚µپC
‚ئژ¦‚³‚ê‚é،A‚ژ‚چ‚‘‚ح‹«ٹEڈًŒڈ‚©‚ç’è‚ـ‚é–¢’è’èگ”‚إ‚ ‚é،‰~“›•ا’†‚ج“_v‚ة”گ¶‚·‚鑬“xƒ|ƒeƒ“ƒVƒƒƒ‹‚ًƒ³T‚ئ‚¨‚پB |
||
|
ƒ³T‚حپC‹‰گ”“WٹJ‚إ
’A‚µپC
‚ئژ¦‚³‚ê‚é،’A‚µپCn‚ژ‚حnژں‚ج‘و“ٌژي‹…ƒxƒbƒZƒ‹ٹضگ”‚XپjپCk‚s‚حâ‘ج•ا’†‚ج”gگ”‚إ‰¹‘¬c‚s‚ئٹpژü”gگ”ƒض‚ً—p‚¢‚ؤk‚s=ƒض/c‚s‚ئژ¦‚³‚êپCB‚ژ‚چ‚‘,C‚ژ‚چ‚‘‚ح‹«ٹEڈًŒڈ‚©‚ç’è‚ـ‚é–¢’è’èگ”‚إ‚ ‚é، چX‚ة‰¹”g‚ھ‰~“›•ا‚ً“§‰ك‚µ‰~“›“à•”‚ضژU—گ‚µ‚ؤ“_‚•‚ة”گ¶‚·‚鑬“xƒ|ƒeƒ“ƒVƒƒƒ‹‚ًƒ³‚c‚ئ‚¨‚،ƒ³‚c‚حپC‰~“›’†گS‚إ—LٹE‚ئ‚ب‚邱‚ئ‚©‚狉گ”“WٹJ‚إپC پ@
’A‚µپC
‚ئژ¦‚³‚ê‚é،D‚ژ‚چ‚‘‚ح‹«ٹEڈًŒڈ‚©‚ç’è‚ـ‚é–¢’è’èگ”پC‚‹D‚ح‰~“›“à”}ژ؟’†‚ج”gگ”‚إkDپپƒضپ^‚ƒDپCپi‚ƒDپF‰~“›“à”}ژ؟‚ج‰¹‘¬پj‚إ‚ ‚é،
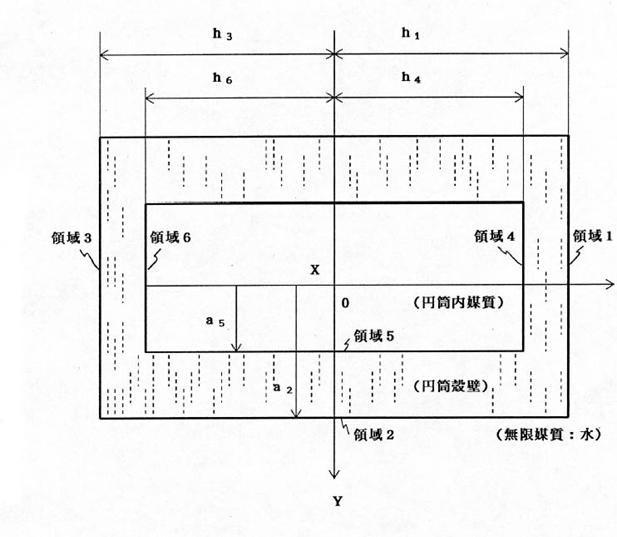
‚QپD‚Qپ@–¢’è’èگ”‚جŒˆ’è ‘Oگك‚إ’èژ®‰»‚µ‚½گ…’†‚ض‚جژU—گ”g‚ج–¢’è’èگ”‚حˆê”ت‚ةٹب’P‚ب‹…ˆبٹO‚ةŒµ–§‰ً‚ھ“¾‚ç‚ê‚ب‚¢پB‘O•ٌ‚Tپj‚إ“K—p‚µ‚½elasticپ@modeپ@analysis‚ً—p‚¢‚éپB گ}‚R‚ة‰~“›‚ج—جˆو•ھٹ„‚ًژ¦‚·پB—جˆو‚PپC‚RپC‚SپC‚U‚ج‰~•½–ت‚ـ‚إ‚جچ‚‚³‚ًگ}‚ج‚و‚¤‚ةپC‚»‚ꂼ‚ꂈ‚PپC‚ˆ‚RپC‚ˆ‚SپC‚ˆ‚U‚ئ‚µ—جˆو‚QپC‚T‚ج‰~“›–ت‚ج”¼Œa‚ًپC‚»‚ꂼ‚ê‚پ‚QپC‚پ‚T‚ئ’è‹`‚·‚éپB
|
|
|
|
گ}‚Rپ@’eگ«‰~“›‚ج—جˆو•ھٹ„ پiYپ|Z–ت“à’f–تگ}پj |
|
–¢’è’èگ”A‚ژ‚چ‚‘پCB‚ژ‚چ‚‘,پ@C‚ژ‚چ‚‘,پ@D‚ژ‚چ‚‘‚ح,ˆب‰؛‚ج‹«ٹEڈًŒڈ‚©‚猈’肳‚ê‚é،—جˆو1پC—جˆو‚QپC—جˆو‚R‚إپC“_‰¹Œ¹‚©‚ç‚جژثڈo”g‚ئ‰~“›•ا‚©‚ç‚ج”½ژث”g‚ج–@گü•ûŒü—±ژq‘¬“x‚جکa‚ھ,‰~“›•ا’†‚ض‚ج‹üگـ”g‚ج—±ژq‘¬“x‚ئ“™‚µ‚¢‚©‚ç,
‚±‚±‚إپC‚ژ‚ح—جˆو•\–ت‚ج–@گü•ûŒü’PˆتƒxƒNƒgƒ‹پC‚r‚†‚ح—جˆو‚†پCپifپپ‚PپC‚QپC‚Rپj‚ج•\–ت‚ًژw‚·ˆت’uƒxƒNƒgƒ‹پC‚ژپق‚ح—جˆو•\–ت‚ج–@گü•ûŒü‚ج”÷•ھŒWگ”‚ً“¾‚鉉ژZژq‚إپC
’A‚µپC‚ژx,‚ژy,‚ژz‚ح,’PˆتƒxƒNƒgƒ‹‚ژ‚جX,Y,Z•ûŒüگ¬•ھ‚إ‚ ‚é، پ@“_‰¹Œ¹‚©‚ç‚جژثڈo”g‰¹ˆ³‚ًP‚‘,ژU—گ”g‰¹ˆ³‚ًP‚’,‰~“›•ا’†‚ض‚ج‹üگـ”g‰¹ˆ³‚ًP‚s‚ئ‚·‚é‚ئ,—جˆو1,2,3‚إپCژثڈo”g‚ج‰¹ˆ³‚ئ‰~“›‚©‚ç‚جژU—گ”g‚ج‰¹ˆ³‚جکa‚ھ‰~“›•ا’†‚ض‚ج‹üگـ”g‚ج‰¹ˆ³‚ئ“™‚µ‚¢‚©‚ç,
ˆê•û,—جˆو4,5,6‚إ,‰~“›“à”}ژ؟‚ج‹üگـ”g‚ج–@گü•ûŒü—±ژq‘¬“x‚ئ‰~“›•ا’†‚ج‹üگـ”g‚ج–@گü•ûŒü—±ژq‘¬“x‚ھ“™‚µ‚¢‚ج‚إ,
‰~“›“à”}ژ؟’†‚ض‚ج‹üگـ”g‰¹ˆ³‚ًP‚c‚ئ‚·‚é‚ئپC‰~“›“à”}ژ؟‚ج‹üگـ”g‚ج‰¹ˆ³‚ئ‰~“›•ا’†‚ج‹üگـ”g‚ج‰¹ˆ³‚ھ“™‚µ‚¢‚©‚ç,
‚ئ‚ب‚é،‚µ‚©‚µپC–¢’è’èگ”‚حˆê”ت‚ةٹب’P‚ب‹…ˆبٹO,Œµ–§‚ة“¾‚ç‚ê‚ب‚¢،‚±‚±‚إ‚حچإڈ¬“ٌڈو–@‚ً—p‚¢‚ؤŒˆ’è‚·‚éپB
‚QپD‚Rپ@چإڈ¬“ٌڈو–@‚ج“K—p پ@ژ®(‚W),(10),(11),(12)‚ة‚¨‚¢‚ؤ,چ¶•س‚©‚ç‰E•س‚ًˆّ‚¢‚½‚à‚ج‚جگâ‘خ’l‚ً,‚»‚ꂼ‚êƒأ1پCƒأ2,ƒأ3پCƒأ4‚ئ‚¨‚‚ئپC
‚±‚±‚إپCƒأ‚PپCƒأ‚QپCƒأ‚RپCƒأ4‚ح—ë‚ئ‚ب‚é‚ׂ«‚à‚ج‚إ‚ ‚é‚ھپCژ®(‚S)پC(‚T)پC(‚U)پC(‚V)‚ج‹‰گ”‚ھ‹…چہ•W‚ج•دگ”‚إ—^‚¦‚ç‚ê,گ}‚R‚ج—جˆو‚PپC‚QپCپDپDپC‚U‚ج‹«ٹE–تŒ`ڈَ‚ً‚±‚ج‹…چہ•W‹ب–ت‚ئˆê’v‚³‚¹‚邱‚ئ‚ھ‚إ‚«‚ب‚¢‚ج‚إŒëچ·‚ًژ‚آپB‚»‚±‚إƒأ‚PپCƒأ‚QپCƒأ‚RپCƒأ‚S‚ج‘S‚ؤ‚ج—جˆو‚ة‚¨‚¯‚é“ٌڈوŒëچ·‚جگد•ھ’lE‚ھچإڈ¬‚ئ‚ب‚é‚و‚¤‚ة–¢’è’èگ”A‚ژ‚چ‚‘پCB‚ژ‚چ‚‘پCC‚ژ‚چ‚‘پCD‚ژ‚چ‚‘‚ًŒˆ’è‚·‚éپBE‚ح
’A‚µپCگد•ھ‹Lچ†“Yژڑ‚ح—جˆو‚ة‚آ‚¢‚ؤ‚ج–تگد•ھپCdsf‚ح—جˆو‚†‚ة‚¨‚¯‚é”÷ڈ¬—v‘f‚ًژ¦‚·پB ‚³‚ç‚ةژ®(17)‚جگد•ھ‚ة•\‚ê‚é’èگ”چ€‚ٹƒض‚ًگد•ھ‚©‚ç‚ح‚¸‚µگâ‘خ’l‚ج‰‰ژZ‚ً•،‘f•\ژ¦‚µپCگV‚½‚ة
|
|
‚ًŒëچ·‚ئ’è‹`‚·‚éپB’A‚µپCپ–‚ح•،‘f‹¤–ً‚ً•\‚·پBژ®پi4پjپCپi‚UپjپCپi8پjپCپi10پj‚ًژ®پi18پj‚ة‘م“ü‚µپC‚dپf‚ج’l‚ھ–¢’è’èگ”A‚ژپf‚چپf‚‘پ–پC‚a‚ژپf‚چپf‚‘پ–پC‚b‚ژپf‚چپf‚‘پ–پC‚c‚ژپf‚چپf‚‘پ–پC‚ج’l‚ةٹض‚ي‚炸چإڈ¬‚ئ‚ب‚é‚و‚¤‚ةپف‚dپf/پفA‚ژپf‚چپf‚‘پ–پCپفEپf/پفB‚ژپf‚چپf‚‘پ–پپ‚O,پفEپf/پفC‚ژپf‚چپf‚‘پ–پپ‚Oپ@پCپفEپf/پفD‚ژپf‚چپf‚‘پ–پپ‚O‚ئ‚¨‚‚ئپCA‚ژپf‚چپf‚‘پ–,B‚ژپf‚چپf‚‘پ–پCC‚ژپe‚چپf‚‘پ–پCD‚ژپf‚چپf‚‘پ–‚ةٹض‚·‚éƒ}ƒgƒٹƒNƒX•û’ِژ®‚ھ“¾‚ç‚ê‚éپB’A‚µپC‚±‚±‚إ‚ح‰و–ت‚ج“sچ‡ڈمپC’èژ®‰»‚µ‚½ƒ}ƒgƒٹƒNƒX—v‘f‚ج•\ژ¦‚ًڈب—ھ‚·‚éپBƒ}ƒgƒٹƒNƒX•û’ِژ®‚ً‰ً‚¢‚ؤپCA‚ژ‚چ‚‘‚ً‹پ‚كژ®پi‚Uپj‚ة‘م“ü‚·‚é‚ئگ…‘…“à‚ة”گ¶‚·‚éژU—گ”g‘¬“xƒ|ƒeƒ“ƒVƒƒƒ‹‚ھ‹پ‚ك‚ç‚êپCژ®پi4پj‚جژثڈo”g‚ئڈd‚ثچ‡‚ي‚¹‚邱‚ئ‚ة‚و‚èچ‡گ¬”g‚ج‘¬“xƒ|ƒeƒ“ƒVƒƒƒ‹ƒ³r‚ھ‹پ‚ك‚ç‚ê‚éپB‚ـ‚½گâ‘خچہ•W‚ج”Cˆس‚ج“_‚—پi‚ک‚—,‚™‚—,‚ڑ‚—پj‚ة‚¨‚¯‚é“ٌ“_‰¹Œ¹‚ة‚و‚éژU—گ”g‰¹ˆ³‚o‚’‚ح,
|
|
‚ئ“¾‚ç‚ê‚éپB’A‚µپCN‚ح‘إ‚؟گط‚èچ€گ”‚إ‚ ‚é، ‚±‚±‚ةپC
‚ئ“¾‚ç‚ê‚éپB
|
|
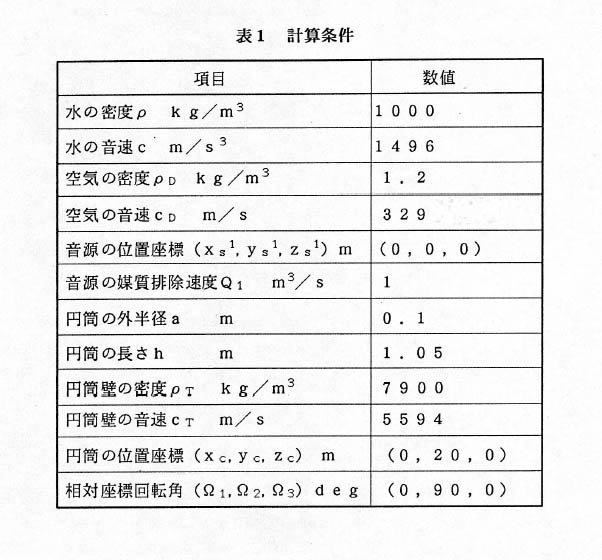
3پDگ”’lŒvژZ—ل‹y‚رŒں“¢ ‰~“›“à”}ژ؟‚ًگ…‚جڈêچ‡‚ئ‹َ‹C‚جڈêچ‡‚ة‚آ‚¢‚ؤ,‰~“›“÷Œْ‚ًƒpƒ‰ƒپپ[ƒ^‚ئ‚µ‚ؤ‰~“›‚جTS‚ً‹پ‚ك‚éپB ‰¹Œ¹‚©‚çگ…’†‚ة‘—”g‚³‚ꂽ‰¹”g‚ح,‰~“›•\–تپi—¼’[–ت‚àٹـ‚قپj‚ة“üژث‚µپCگ…‚ئ‰¹‹؟ƒCƒ“ƒsپ[ƒ_ƒ“ƒX‚جˆظ‚ب‚é‰~“›•\–ت‚©‚çˆê•”‚ھ”½ژث‚³‚ê‚éپBˆê•û‚إ“üژث‚µ‚½‰¹”g‚ح‰~“›•ا‚ض‚ئ‹üگـ“§‰ك‚µپC‰¹‹؟ƒCƒ“ƒsپ[ƒ_ƒ“ƒX‚جˆظ‚ب‚é‰~“›“à”}ژ؟‚©‚çˆê•””½ژث”g‚ھ”گ¶‚·‚éپB‚±‚±‚إ‰~“›“à”}ژ؟‚ً“`”d‚µ‚½”g‚حچX‚ة‰~“›•ا‚©‚甽ژث‚ًژَ‚¯‚éپB‰¹Œ¹‘¤‚ة‚حپC‚±‚ج‚و‚¤‚ة”½ژث‚³‚ꂽ”g‚جˆê•”‚ھ“`”d‚³‚ê‚邱‚ئ‚ئ‚ب‚éپBTS‚حپC‰¹Œ¹‚©‚çڈo‚½”g‚ج‹‚³‚ة‘خ‚·‚锽ژث‚³‚ê‚ؤ–ك‚ء‚ؤ‚«‚½”g‚ج‹‚³‚ج”ن‚ج‘خگ”’l‚إ—^‚¦‚ç‚ê‚éپB‚µ‚½‚ھ‚ء‚ؤTS‚ھ‚O‚„B‚جڈêچ‡‚حٹ®‘S”½ژث‚جڈêچ‡‚ئ‚ب‚éپBTS‚ھ‚O‚„Bˆبڈم‚ج’l‚ًژ¦‚·ڈêچ‡‚ح,‹¤گU‚ة‚و‚è‰~“›‚ھگV‚½‚ب‰¹Œ¹‚ئ‚ب‚éڈêچ‡‚إ‚ ‚éپB–{گ”’lŒvژZ‚ة‚¨‚¢‚ؤ‚ح,ˆê—ل‚ئ‚µ‚ؤ‰¹Œ¹‚ًˆêŒآ‚ئ‚µ,‰¹Œ¹‚ئ‰~“›‚ج‹——£‚ً‰~“›چ‚‚³‚ة”ن‚בه‚«‚‘I‚ٌ‚¾پB‚ـ‚½,‰~“›ٹOŒa‚ة”ن‚ׂؤ‰~“›چ‚‚³‚ً‘ه‚«‚‘I‚ٌ‚¾پB•\‚P‚ةŒvژZڈًŒڈ‚ًژ¦‚·پB |
||||
|
|
||||
|
‰~“›“à”}ژ؟‚ًگ…‚ئ‚µ,‰~“›“÷Œْ‚Tmm,‚P‚Omm,‚S‚Omm‚ئ‚µ‚½ڈêچ‡‚جTS‚ًگ}‚S‚ةژ¦‚·پB‰،ژ²‚ح–³ژںŒ³ژü”gگ”پiگ…‚ج”gگ”k‚ئ‰~“›ٹO”¼Œa‚پ‚جگدپj‚إ‚ ‚éپBچ،,‚پ=0.1‚چپC‚ƒ=1496‚چ/‚“‚إ‚ ‚é‚©‚ç,ka=‚Qƒخf‚پپ^‚ƒ=4.2پ~10پ\4‚†پi‚½‚¾‚µf‚حژü”gگ”پj‚ئ‚ب‚éپB‚±‚ê‚ة‚و‚èٹ·ژZ‚·‚é‚ئ‰،ژ²‚جka=1.2‚ح2.85KHz‚إ‚ ‚éپB1KHzˆب‰؛‚ج’لژü”g‚ًگفŒvڈم‘خڈغ‚ئ‚·‚é‚ب‚ç‚خ,kaپƒ0.42‚ج”حˆح‚إ‚ ‚é‚ھ,‚±‚±‚إ‚ح‚»‚êˆبڈم‚جژü”gگ”‚ة‚àگG‚ê‚ؤTS‚ًŒں“¢‚·‚邱‚ئ‚ئ‚µ‚½پBگ}’†,ژہگü‚ح–{ژè–@پielasticپ@modeپ@analysisپj‚ً—p‚¢‚½ڈêچ‡‚إ‰~“›“÷Œْ40mm‚جڈêچ‡,’·‚¢”jگü‚ح‰~“›“÷Œْ10mm‚جڈêچ‡پC’Z‚¢”jگü‚ح‰~“›“÷Œْ5mm‚جڈêچ‡‚إ‚ ‚éپB |
||||
|
|
||||
|
گ}‚Sپ@‰~“›“à”}ژ؟‚ًگ…‚ئ‚µ,‰~“›“÷Œْ‚ً•د‚¦‚½ڈêچ‡‚جTS پ|پ|‰~“›“÷ŒْپF‚Tmm پ\ پ\‰~“›“÷ŒْپF‚P0mm پ|‰~“›“÷ŒْپF40mm
|
||||
|
گ}‚©‚ç”»‚é‚و‚¤‚ة,Ka‚ھڈ¬‚³‚¢—جˆوپi‚‹‚پ<0.3پj‚إ‚ح,‚ظ‚ع‰~“›“÷Œْ‚ة‚و‚ç‚ب‚¢TS‚ًژ¦‚·پBˆê•ûka‚ھ‘ه‚«‚‚ب‚é‚ئ,“÷Œْ‚جŒْ‚¢•û‚ھڈ‚µچ‚‚¢TS‚ًژ¦‚·پB‚±‚ê‚حپC‰~“›•اŒْ‚فگU“®‚ج”گ¶‚·‚éژü”gگ”‚ة”ن‚×پCڈ\•ھ’ل‚¢ژü”gگ”‚ةŒ©‚ç‚ê‚é‚à‚ج‚إژ؟—ت‘¥‚ً—p‚¢‚ؤگà–¾‚إ‚«‚éپB‚±‚ê‚ة‚و‚é‚ئپC‰~“›•ا‚ج“§‰ك‘¹ژ¸پi[‰~“›ٹk“à‘¤‚ج‰¹ˆ³PTپ^‰~“›ٹk‚جٹO‘¤‚ج“üژث‰¹ˆ³PI]‚ج‹tگ”‚جƒfƒVƒxƒ‹’l‚إ’è‹`‚³‚ê,10logپiPT/PIپjپ|‚Q‚إژZڈoپj‚حپC’Pˆت–تگد•س‚è‚ج‰~“›•اژ؟—ت‚ةˆث‘¶‚µ,Œْ‚¢چق—؟‚ظ‚ا‘ه‚«‚‚ب‚邱‚ئ‚ھ’m‚ç‚ê‚ؤ‚¢‚éپB“§‰ك‘¹ژ¸‚ھ‘ه‚إ‚ ‚é‚ئ, PT/PI‚ج’l‚ھڈ¬‚إ‚ ‚é‚©‚瓧‰ك‰¹ˆ³‚ھڈ¬‚³‚¢پBŒ¾‚¢ٹ·‚¦‚ê‚خ‰~“›•\–ت‚إ”½ژث‚³‚ê‚â‚·‚¢پB‚µ‚½‚ھ‚ء‚ؤTS‚ج’l‚ھ‘ه‚«‚‚ب‚éپB‚µ‚©‚µ,“÷Œْ5mm‚ئ40mm‚ج‰~“›‚إپCTS‚حڈ‚µ‚جˆل‚¢‚µ‚©Œ»‚ê‚ب‚¢‚و‚¤‚إ‚ ‚éپB ‚ـ‚½گ}’†,‚‹‚پ‚ھ1.2•t‹ك‚إچ‚‚¢TS‚ًژ¦‚·‚ج‚ح,‰~“›چ‚‚³•ûŒü‚ج‹¤گU‚ج‰e‹؟‚إ‚ ‚éپBچ‚‚³•ûŒü‚جˆêژں‹¤گUژü”gگ”11پj‚حپC‰~“›’[–ت‚ًچا‚®‰~”آژ؟—ت‚ًچl‚¦‚ب‚¢‚ئCTپ^پi2‚ˆپjپپ2.67‚j‚g‚ڑ‚ئ‚ب‚èپC‚±‚ج‚ئ‚«‚‹‚پپپ1.12‚ئ‚ب‚邱‚ئ‚©‚ç”»’f‚³‚ê‚éپB‚‹‚پ‚ھ1.2ˆب‰؛‚إ‚àƒXƒvƒٹƒAƒX‚بƒ‚پ[ƒh‚ھ”گ¶‚·‚é‚ج‚إ‚s‚r‚ج’l‚ح‘ه‚«‚‚ب‚é‚و‚¤‚إ‚ ‚éپBپ@ گ}‚Tپ|1,گ}‚Tپ|2,گ}‚Tپ|3‚ةپC‰~“›“à”}ژ؟‚ً‹َ‹C‚ئ‚µپC‚»‚ꂼ‚ê‰~“›“÷Œْ‚ً5mm,‚P0mm,40mm‚ئ•د‚¦‚½‚ئ‚«‚جTS(”jگü)‚ًژ¦‚·پB‚ب‚¨”نٹr‚ج‚½‚ك‚»‚ꂼ‚ê‚جگ}‚ة‰~“›“à”}ژ؟‚ًگ…‚ئ‚µ‚½‚s‚r(ژہگü)‚àڈ‘‚«‰ء‚¦‚½پB
|
||||
|
|
|
|||
|
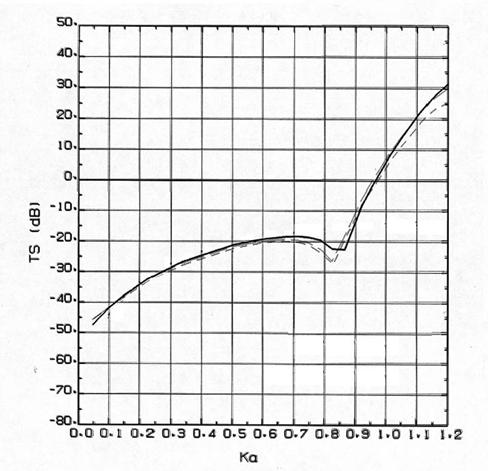
گ}5پ|1پ@‰~“›ٹk“÷Œْ‚ً5mm‚ئ‚µ‚½‚s‚r پ|پ|‰~“›“à”}ژ؟پF‹َ‹C پ|‰~“›“à”}ژ؟پFگ…
|
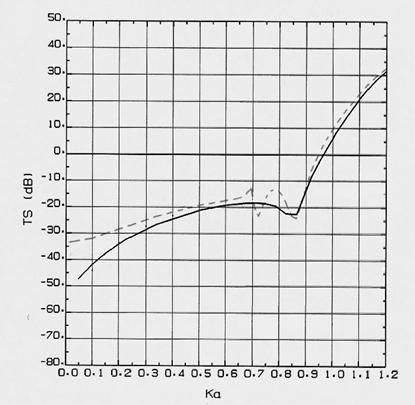
گ}5پ|2پ@‰~“›ٹk“÷Œْ‚ً10mm‚ئ‚µ‚½‚s‚r پ|پ|‰~“›“à”}ژ؟پF‹َ‹C پ|‰~“›“à”}ژ؟پFگ… |
|||
|
|
‚±‚ê‚ç‚جگ}‚©‚ç,‰~“›“à”}ژ؟‚ھگ…‚و‚è‚à‹َ‹C‚ج•û‚ھچ‚‚¢TS‚ًژ¦‚·‚±‚ئ‚ھ”»‚éپB‚±‚ê‚حپC‹َ‹C‚ج‰¹‹؟ƒCƒ“ƒsپ[ƒ_ƒ“ƒX(پپ3.95پ~102kg/(m2s))‚ھگ…‚â‰~“›•ا”}ژ؟‚ة”ن‚ׂؤ‹ة’[‚ةڈ¬‚³‚¢‚ج‚إ,”½ژث‚ھ‘ه‚«‚‚ب‚邽‚ك‚إ‚ ‚éپB‰~“›‚جٹO”¼Œa‚ئچ‚‚³‚ًچ،Œإ’肵‚ؤ‚¢‚é‚©‚ç,‰~“›“÷Œْ‚ًŒْ‚‚·‚邱‚ئ‚ح‰~“›“à‹َ‹C‚ج—ت‚ًŒ¸‚ç‚·‚±‚ئ‚ئ“¯‚¶‚إ‚ ‚éپB‚±‚ج‚ئ‚«گ}5پ|3‚ج‚و‚¤‚ة‰~“›“à”}ژ؟‚ھگ…‚جڈêچ‡‚جTS‚ة‹ك‚¢’l‚ًژ¦‚·‚و‚¤‚إ‚ ‚éپB‚µ‚©‚µپCka‚ھ0.3ˆب‰؛‚ج’لژü”g‚إ‚ح,‹َ‹C‚ج•û‚ھچ‚‚¢TS‚ًژ¦‚·پB‚±‚ê‚ح‰~“›“à”}ژ؟‚ھگ…‚جڈêچ‡پC’لژü”g‚إ‚ ‚é‚ئ‰~“›ٹk‚ج“÷Œْ5mm‚إ‚à40mm‚إ‚àTS‚ھ’ل‚ڈo‚½‚±‚ئ‚©‚çگà–¾‚إ‚«‚éپBka<0.3‚ج—جˆو‚ح‰~“›•ا‚ج“§‰ك‘¹ژ¸‚ھڈ¬‚³‚‰~“›“à‚ض‚ج‰¹”g“§‰ك—ت‚ھ‘‚·—جˆو‚إ |
|||
|
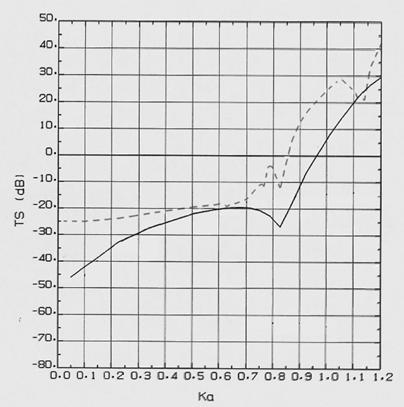
گ}5پ|3پ@‰~“›ٹk“÷Œْ‚ً‚S0mm‚ئ‚µ‚½‚s‚r پ@پ@پ|پ|‰~“›“à”}ژ؟پF‹َ‹C پ|‰~“›“à”}ژ؟پFگ… |
||||
|
‚ ‚ء‚½پB‚·‚é‚ئپC‰¹‹؟ƒCƒ“ƒsپ[ƒ_ƒ“ƒX‚ج‹ة’[‚ةڈ¬‚³‚¢‰~“›“à”}ژ؟‚ج‹َ‹C‚ة‚و‚锽ژث”g‚ھˆ³“|“I‚ةگè‚ك‚邱‚ئ‚ة‚ب‚éپBگ}5پ\1,گ}5پ\2,گ}5پ\3‚ً’ت‚µ‚ؤ‚ف‚é‚ئ, ‚±‚ج”½ژث”g‚ح”–“÷‚ج‰~“›‚إ‹َ‹C‚ج—ت‚ھ‘½‚¢‚ظ‚ا‹‚چ‚‚¢TS‚ًژ¦‚·پB پ@‚±‚ê‚ـ‚إ‚جŒ‹‰ت‚©‚ç,‰~“›“à”}ژ؟‚ھگ…‚ج‚ئ‚«,‰~“›•ا“÷Œْ‚ًŒْ‚‚µ‚ؤ‚à‚ ‚ـ‚èTS‚ھ‘ه‚«‚‚ب‚ç‚ب‚¢‚±‚ئ‚ھ”»‚ء‚½پB‚آ‚ـ‚蔽ژث‚ح‚»‚ê‚ظ‚ا–â‘è‚ب‚¢پBˆê•û,‰~“›“à”}ژ؟‚ھ‹َ‹C‚جڈêچ‡پC”–“÷‚ج‰~“›‚إ‚ح,‹َ‹C‚ج”½ژث‚ھ‹‚‚ب‚邱‚ئ‚ھ”»‚ء‚½پB‰~“›“à”}ژ؟‚ھ‹َ‹C‚ج‚ئ‚«‚ح‹َ‹C—eگد‚ًŒ¸‚炳‚ب‚¢Œہ‚è,”½ژث‚ً’لŒ¸‚إ‚«‚ب‚¢‚à‚ج‚ئچl‚¦‚éپB |
||||
|
‚SپD‚ـ‚ئ‚ك پ@‰¹Œ¹‹ك–T‚ة‘•”ُ‚³‚ê‚é‰~“›—eٹي‚©‚ç‚ج‰¹”g”½ژث‰e‹؟‚ً’²‚ׂ邽‚كٹî–{Œں“¢‚ئ‚µ‚ؤ,گو‚ةچ\’z‚µ‚½‰¹Œ¹’P‘ج‚ج‰¹ڈê‰ًگحژè–@elasticپ@modeپ@analysis‚ً‰~“›—eٹي‚ة“K—p‚µژU—گ‰¹ڈê‰ًگح‚ًچs‚ء‚½پB‰~“›—eٹي‚جچ‚‚³•ûŒü‚ج‹¤گUژü”gگ”ˆب‰؛‚إ‚ح,‰~“›“à•”‚ًگ…‚ئ‚µ‚½ڈêچ‡,’لژü”g‚إŒْ“÷‚إ‚à—eˆص‚ة‰¹”g“§‰ك‚·‚邱‚ئ,‰~“›“à‚جگ…‚©‚ç‚ج”½ژث‚ھ–³‚TS‚ھ’ل‚¢‚±‚ئپCTS‚ح‰~“›“÷Œْ‚ج•د‰»‚ة‚و‚è‚ ‚ـ‚è•د‰»‚µ‚ب‚¢‚±‚ئ‚ھ”»‚ء‚½پB‰~“›“à”}ژ؟‚ھگ…‚ب‚ا‰t‘ج‚إ‚ ‚ê‚خ,”½ژث‚ج–â‘è‚ح–³‚¢‚ئژv‚ي‚ê‚éپB ‚µ‚©‚µپC‰~“›“à•”‚ھ‹َ‹C‚ب‚ا‚ج‹C‘ج‚جڈêچ‡,‹َ‹C‚©‚çچ‚‚¢”½ژث”g‚ھ”گ¶‚·‚éپB’لژü”g‚إ—eٹي‚©‚ç‚ج”½ژث‚ًŒ¸‚ç‚·‚ة‚ح,‰~“›“÷Œْ‚ًŒْ‚‚·‚é‚و‚è‚à“à•”‚ج‹َ‹C—ت‚ًŒ¸‚ç‚·•û‚ھŒّ‰ت“I‚إ‚ ‚éپB
•tک^پ@DCM‚جŒ‹‰تŒں“¢ پ@ژQچl‚ئ‚µ‚ؤ, Stanton‚ة‚و‚ء‚ؤ’ٌˆؤ‚³‚ê‚ؤ‚¢‚éٹبˆص“I‚بژU—گ‰ًگحژè–@‚ة‚و‚éTS(deformedپ@cylinderپ@solutionپ@method‚S)پC‚±‚±‚إ‚حDCM‚ئŒؤ‚ش‚±‚ئ‚ة‚·‚é)‚ئ–{ŒvژZ’l‚ج”نٹr‚ًژ¦‚·پB DCM‚ة‚آ‚¢‚ؤ‚حˆب‰؛‚ج“K—pڈًŒڈ‚ھ‚ ‚éپB ‚P) ‰~“›’·‚³/‰~“›ٹO”¼Œa‚ج’l‚ھ‘ه‚«‚¢ڈêچ‡,‚·‚ب‚ي‚؟چ×’·‚¢ڈêچ‡‚ًژو‚舵‚¦‚éپB ‚Q) ‰~“›‚جژ²•ûŒü‚ج‹«ٹEڈًŒڈ‚ح–³Œہ‰~“›‚جڈêچ‡‚ئ“¯‚¶‚ئ‚·‚éپB‚·‚ب‚ي‚؟ژ²•ûŒü‚ج‰¹ˆ³•ھ•z‚ب‚ا‚ھٹة‚â‚©‚ة•د‰»‚µژ²•ûŒü‚ة’¼ٹp‚ة—ضگط‚è‚ة‚µ‚½‚»‚ꂼ‚ê‚ج”÷ڈ¬•”•ھ‚ح,—ד¯ژu‚إ“™‚µ‚¢“®‚«‚ً‚·‚é‚à‚ج‚ئ‚·‚éپB ‚R) “üژث”g‚ح,‰~“›ژ²‚ةگ‚’¼‚©‚ظ‚عگ‚’¼‚ة“—ˆ‚·‚é‚à‚ج‚ئ‚·‚éپB ‚S) —LŒہ’·‰~“›‚ج’[–ت‚ج‰e‹؟‚ًچl‚¦‚ب‚¢پB ‚T) ‰~“›‚ة‚¨‚¢‚ؤ,ژ²•ûŒü•دˆت‚ئŒa•ûŒü•دˆت‚حژ²•ûŒü‚ة‚ب‚¾‚ç‚©‚ة•د‰»‚·‚é‚à‚ج‚ئ‚·‚éپB ‚U) —LŒہ’·‰~“›‚ئ‰¹Œ¹ٹش‹——£‚حپC—LŒہ’·‰~“›‚ج’·‚³‚ة”ن‚ׂؤڈ\•ھ‘ه‚«‚¢پiƒtƒŒƒlƒ‹—جˆو‚جڈًŒڈ‚ً–‘«پj‚ئ‚·‚éپB
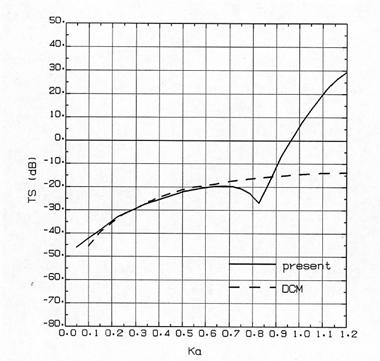
•tگ}1پC•tگ}2‚ة‰~“›“à”}ژ؟گ…پC‰~“›“÷Œْ5mmپC10mm‚ة‚آ‚¢‚ؤ‚ج–{ژè–@‚ئDCM‚ج”نٹr‚ًژ¦‚·پBگ}’†,ژہگü‚ح–{ژè–@پipresent‚ئ•\ژ¦پjپC”jگü‚ح‚c‚b‚l‚جŒ‹‰ت‚إ‚ ‚éپB |
||||
|
|
|
|||
|
•tگ}1پ@–{ژè–@‚ئDCM‚ج”نٹr (‰~“›“à”}ژ؟پFگ…,“÷Œْ5mm) |
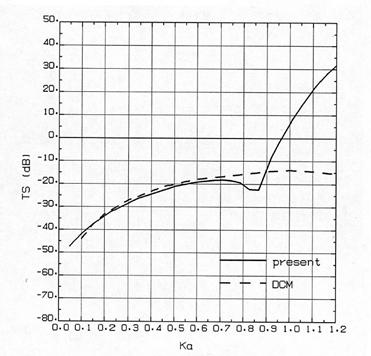
•tگ}‚Qپ@–{ژè–@‚ئDCM‚ج”نٹr (‰~“›“à”}ژ؟پFگ…,“÷Œْ10mm) |
|||
|
•tگ}‚PپC•tگ}‚Q‚©‚çپC‚‹‚پ‚ھ0.7ˆب‰؛‚ة‚¨‚¢‚ؤ—¼ژز‚ح‚ظ‚عچ‡‚ء‚ؤ‚¢‚éپBˆê•ûDCM‚إ‚ح, “K—pڈًŒڈ‚©‚ç‰~“›ژ²•ûŒü‚ج‹¤گU‚ھŒ»‚ê‚ب‚¢پB‚µ‚©‚µپC‚‹‚پپƒ0پD7’ِ“x‚ج’لژü”g‚إ‚حDCM‚ھژg‚¦‚é‚ئژv‚ي‚ê‚éپB |
||||
|
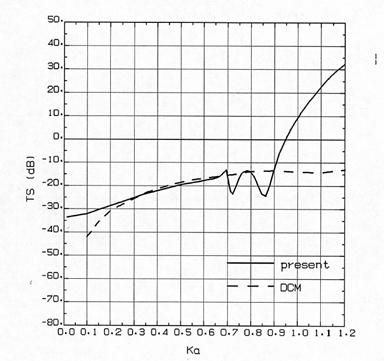
•tگ}‚RپC•tگ}‚S‚ة‰~“›“÷Œْ‚S‚Omm‚جڈêچ‡‚إپC‰~“›“à”}ژ؟‚ًگ…‚ئ‚µ‚½ڈêچ‡‚ئ‹َ‹C‚ئ‚µ‚½ڈêچ‡‚ج–{ژè–@‚ئDCM‚ج”نٹr‚ًژ¦‚·پB |
||||
|
|
|
|||
|
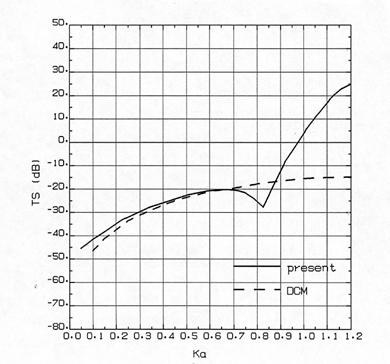
•tگ}‚Rپ@–{ژè–@‚ئDCM‚ج”نٹr (‰~“›“à”}ژ؟پFگ…,“÷Œْ40mm) |
•tگ}‚Sپ@–{ژè–@‚ئDCM‚ج”نٹr (‰~“›“à”}ژ؟پF‹َ‹C,“÷Œْ40mm) |
|||
|
•tگ}‚R,•tگ}‚S‚©‚ç,‰~“›“à”}ژ؟‚ھگ…‚جڈêچ‡پC‚‹‚پپƒ0.7‚ج”حˆح‚إ–{ژè–@‚ئ‚c‚b‚l‚ح‚و‚چ‡‚ء‚ؤ‚¢‚é‚ھ,‰~“›“à”}ژ؟‚ھ‹َ‹C‚جڈêچ‡‘ٹˆل‚ھ‚ ‚èپC‚‹‚پپƒ0.2‚ج”حˆح‚إ‚c‚b‚l‚جTS‚ح‚و‚è’ل‚ك‚ةڈo‚éپB‚ـ‚½DCM‚إ‚ح,‰~“›“à•”‚ھگ…‚إ‚à‹َ‹C‚إ‚à“¯‚¶Œ‹‰ت‚إ‚ ‚éپB پ@Stanton‚جTSŒvژZ–@‚حٹب’P‚إ‚à‚ ‚è,ڈًŒڈ‚³‚¦چ‡‚¦‚خژg—p‚إ‚«‚é‚ئژv‚ي‚ê‚é‚ھپCژہچغ‚ج‚ئ‚±‚ë‚»‚جڈًŒڈ‚ً–‘«‚إ‚«‚é‚©‚ا‚¤‚©”»’f‚ھ“‚¢پB‚±‚جTSŒvژZ–@‚ة‚آ‚¢‚ؤ,Partridge‚ئSmith12)‚حپCگ¸“x‚جŒں“¢‚ًچs‚ء‚ؤ‚¢‚éپBˆê•û,Sommerfeldپ|Watson•دٹ·–@‚ً—p‚¢‚½TSŒvژZ–@‚إ,Ruemern13),14)‚حDCM‚ئ‚ج”نٹr‚ً‚µ‚ؤ‚¢‚éپB‚±‚ê‚ة‚و‚é‚ئپC‰~“›“à”}ژ؟‚ھ‹َ‹C‚ج‚ئ‚«پCDCM‚جŒ‹‰ت‚و‚èچ‚‚¢TS‚ج“¾‚ç‚ê‚邱‚ئ‚ھژ¦‚³‚ê‚ؤ‚¢‚éپB |
||||
|
•¶Œ£ 1پj Robert Hickling,پhAnalysis of Echoes from a Solid Elastic Sphere in Water,پh J.Acoust.Soc.Am.34(10),‚گ1582-1592,(1962) 2پj Tai-bao Li and Mitsushiro Ueda,پhSound scattering of spherical wave incident on a cylinder,پhJ.Acoust.Soc.Am.87,p1871-1879,(1990) 3پj Tai-bao Li and Mitsushiro Ueda,پhAnalysis of echoes from a cylinder that includes the directivity of the transmitter and receiver,پhJ.Acoust.Soc.Am.87,p1880-1884,(1990) 4) T.K.Stanton,پhSound scattering by spherical and elongated shelled bodies,پh J.acoust.Soc.Am.88(3).‚گ1619-1633,(1990) 5پjƒgƒsƒbƒNƒX‚P‚PپCپw‰~“›Œ^’لژü”g‰¹Œ¹‚جژwŒüگ«پ|گ…‘…‚إ‚جژہ‘ھ’l‚ئŒvژZ’l‚ج”نٹrپxپiپf‚O‚RپD‚QپD‚Rپj 6پjƒgƒsƒbƒNƒX‚P‚Rپw‰~“›Œ^’لژü”g‰¹Œ¹‚ج‘—”g‰¹ˆ³‚جŒں“¢-‚Pپi‰~“›ٹO”¼Œa‚ً•د‚¦‚½ڈêچ‡پjپxپiپf‚O‚RپD‚XپD‚Q‚Wپj 7پjƒgƒsƒbƒNƒX‚P‚Sپw‰~“›Œ^’لژü”g‰¹Œ¹‚ج‘—”g‰¹ˆ³‚جŒں“¢-‚Qپi‰~“›â‘جچ‚‚³‚ً•د‚¦‚½ڈêچ‡پjپxپiپf‚O‚RپD‚P‚QپD‚Q‚Xپj ‚Wپj‘پچâژُ—Y,‹gگىڈ؛‹gکY,‰¹‹؟گU“®ک_,(ٹغ‘P(ٹ”),“Œ‹,1974),‚گ501پ|503 ‚XپjگXŒû”ةˆê,‚ظ‚©2–¼,گ”ٹwŒِژ®‡V,“ءژêٹضگ”,(ٹâ”gڈ‘“X,“Œ‹,1977),‚گ218-220 ‚P‚Oپj•¶Œ£‚X),‚گ137 ‚P‚Pپj‰œ“‡ٹî—اپCپhƒ`ƒ^ƒoƒٹ‰~“›ٹk‚ً—p‚¢‚½گ…’†‘ٹŒفچZگ³—p•âڈ•‘—ژَ”gٹيپh,“ْ–{‰¹‹؟ٹw‰ïژڈ,‘و17چ†,‘و4ٹھ,(1961) 1‚QپjChris partridge and edgar R.Smith,پhAcoustic scattering from bodies: Range of validity of the deformed Cylinder method,پhJ.Acoust.Soc.Am.,Vol.97(2),P784-795,(1995) 1‚R) M.L.Ruemern,پhApplication of the Sommerfeld-Watson transformation to scattering of acoustic wave obliquely incident upon cylindrical shells,پh J.Acoust Soc.Am .,Vol.91,p2502-2509,(1991) 1‚S) M.L.Ruemern,پhIncreased Accuracy in the application of Sommerfeld-Watson transformation to acoustic scattering from cylindrical shells,پhJ.Acoust.Soc.Am,Vol.90,p2739-2751,(1990)
|
||||
|
|
|
|||
|
||||