|
|
|
�g���ɔ�ׂđ傫�����@�̖��ݕ��͂悭�g�˂���B���Ȃ킿�g�͉�܂��čs���Ȃ��B���̂��Ƃ́C�e�Ղɑz�������B������������������Ƃ�����������g�͉�荞�߂Ȃ�����ł���B����ł́C���ݕ��̐��@�������ōގ����Ⴄ�ƁC���˔g�̋����͂ǂ��Ȃ邾�낤���H��̃y�[�W�Ŕ}���Ɩ��ݕ��̕������قȂ�Ɣ��˔g�������C�ŏI�I�ɖ��ݕ������o����Əq�ׂ��B�����ł͊ȒP�̂��ߔ}���𐅂Ƃ��C�����ɒ��߂�ꂽ�����ȍޗ�����Ȃ�^�[�Q�b�g�i�����ōl����̂Ŗ��ݕ��ƌ�������Ƀ^�[�Q�b�g�ƌĂԁj���āC���˔g�̏o��ׂ�B |
|
|
|
|
�^�[�Q�b�g�͐F��Ȍ`���Ȃ�����B�����ł͊ȒP�ȗ�Ƃ������`�Ƃ���B��ʂɃ^�[�Q�b�g���ő̂̏ꍇ�C�g��������ƃ^�[�Q�b�g���ɒe���g(�c�g�Ɖ��g)���������顂����ł��@�e���g�i�c�g�Ɖ��g�j���l�������ꍇ���A�c�g�̂ݍl�������ꍇ�ɂ��āC���˔g���v�Z����B�^�[�Q�b�g�́C�c�g���x�C���g���x�̑������̂���x�����́C���x�̑傫�����̂��珬�������̂܂Ŏ�ނ�ς���B���˔g�͔g���������̋������ŋ��߂�B ���˔g�̒��x���`�F�b�N�ł���L���Ȏ�@�Ƃ��āC�e�����̔��ˌW���ׂ���@������B�ȒP�Ɍ����ƁC�_�������瑗�o�������g���C�����ɒu���ꂽ�����̍d���������Ŕ��˂���_�����̈ʒu�ɖ߂��Ă������g�̋������O�����߁C�����������Ɠ����ʒu�ɒu���ꂽ�e�����Ŕ��˂���_�����̈ʒu�ɖ߂��Ă������g�̋����ӂ������߁C�ӂ��ƃ��O�̔�i��s�^���O�j���Ƃ���@�ł���B���̒l�͔��ˌW���ЂƂ��Ē�`�����B���Ȃ킿�C�����̍d���������ł���Ί��S���˂��邩��_�����̈ʒu�ɖ߂�g�̃��x���͂��Ƃ̔g�̃��x���Ɠ����ɂȂ蔽�ˌW���Ђ͂P�ƂȂ�B�������ɂ���ƒe�����̔��˂̓x����������̂ł��顎��ہC�e��������������菬���������܂��Ċg�U���čs���g�i�O���U���g�ƌĂԁj���l������B����Œe�����́C�e���������Ă��邪�䂦�ɁC������g���ŋ��U���傫�Ȕ��˔g�ޏꍇ�����顂��̂Ƃ����ˌW���Ђ͂P�ȏ�ƂȂ�B�����͌v�Z���邱�Ƃɂ���Ĕ����\�P�Ɍv�Z�ɗp�����e�����̍ޗ��萔�������B���}���i���j�̖��x�͂P�O�O�Ok���^���R�C�c�g���x�����P�S�P�O���^���Ƃ����}���`�}���ɕ\�P�̊e�ޗ���p�����^�\�Q�b�g�̔��ˌW������������������̂�����,�}���̔g�����ƒe�����̔��a���̐ρi���������ƂȂ�j�ŕ\��������Ŕg������,���g�����Ɣ}���̏c�g���x����p���Ă����Q���^���Ǝ�����,���̂Ƃ��̔g���ɂ�p���Ă����Q�^�ɂƎ�����顂��Ȃ킿���g�����ł�����傫�Ȓl�ɕω������邱�Ƃ́C�e�����̔��a��傫���ω������邱�Ƃɑ�����,�e�������a���ł�����傫�Ȓl�ɕω������邱�Ƃ́C���g���������ق��ɕω������邱�Ƒ������顔��ˌW���ɂ��āC�����C���s�[�_���X�ɂ�錟�����������B�}���ƃ^�[�Q�b�g�̍ޗ��̈Ⴂ�ɂ�鉹�g�̓��ߓx�����f����ڈ��Ƃ��āC�����C���s�[�_���X������B �}���ƃ^�[�Q�b�g�̖��x���߂���C�܂��}���ƃ^�[�Q�b�g�̏c�g���x���߂���C���g�͗��҂߂��₷�����낤�B�ɒ[�ȏꍇ�C�܂������}���Ɠ������̂��^�[�Q�b�g�ł���Ή��g�̔��˂͖����B�������߂̂��₷���������ڈ��Ƃ��Ė��x�Əc�g���x�̐ςŕ\���ʂ������C���s�[�_���X�ł���B |
|
�\�P�@�ޗ��萔 |
||||
|
�e�����ޗ� |
���x�i�����^���R�j |
�|�A�\���� |
�c�g���x�i���^���j |
���g���x�i���^���j |
|
�x�����E�� |
�P�W�V�O |
�O.�O�T |
�P�Q�W�X�O |
�W�W�W�O |
|
�Z��Ήp�i�N�E�H�[�c�j |
�Q�Q�O�O |
�O.�P�V |
�T�X�U�W |
�R�V�U�S |
|
�S |
�V�V�O�O |
�O.�Q�X |
�T�X�U�O |
�R�Q�S�O |
|
�A���~�j�E�� |
�Q�V�O�O |
�O�D�R�T�T |
�U�S�Q�O |
�R�O�S�O |
|
�^�J |
�W�U�O�O |
�O�D�R�V�S |
�S�V�O�O |
�Q�P�P�O |
|
���[�T�C�g�i�A�N���������j |
�P�P�W�O |
�O�D�S |
�Q�U�W�O |
�P�P�O�O |
|
��C |
�P.�Q |
�| |
�R�S�O |
�| |
|
���ˌW���̌v�Z���� |
|
�}���@�x�����E�����̔��ˌW�� |
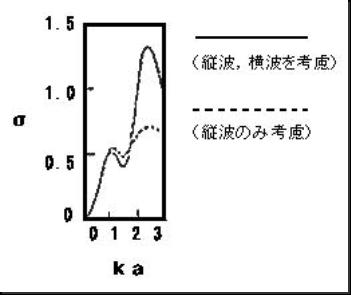
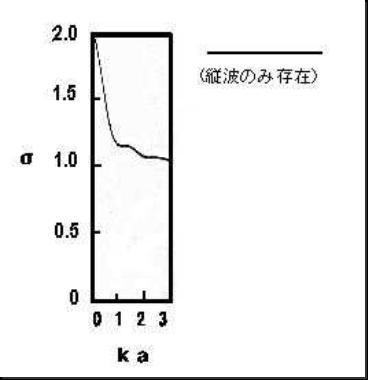
�c�g�����g���l�������v�Z���� �������P�Ŕ��ˌW���̈�Ԗڂ̋��U�s�[�N������顃Ё�0.5�ł��顂�����1�ł́C���̑S�������傤�Lj�g���ɑ������C���ɐ����ē��˂��鉹�g�����̉E�ƍ��ł��傤�ǔ��g����܂������ƂƂȂ顂�����2�ŃЁ�1�ƂȂ芮�S���˂��N���顂�����2.2�ő��̋��U���N����Ё�1.2�ł��顂��������̋��U�͂�����2��荂�߂ł��邩��,���ˉ��g�����������g���ȏ��܂��ē��U���������顋��̏ꍇ�C�������{�X�ƂȂ�Ƃ���ɋ��U������Ȃ��悤�ł��� �c�g�݂̂��l�������v�Z���� �������P�Ŕ��ˌW���̈�Ԗڂ̋��U�s�[�N������顏c�g�Ɖ��g���l�������ꍇ�Ɠ������C���̃Ђ̒l��0.5�ł��額X���c�g�Ɖ��g���l�������ꍇ���C�c�g�̂ݍl�������ꍇ��,���ˌW���͂�����1.8�ȉ��͈̔͂łقƂ�Ǔ����ł��顂��������āC���͈̔͂ł͉��g�̉e�����Ȃ����Ƃ��������,������1.8�ȏ�ł�,�c�g�Ɖ��g���l�������ꍇ�ɔ�ׂč����傫������ˌW���̑��̃s�[�N�͍��X�Ё�0.7�Ɏ~�܂�B������1.8�ȏ�ł͉��g���x�����E�����̏c�g�U���ɃJ�b�v�����O���傫�ȐU��������ƍl������ �����C���s�[�_���X�ɂ�錟�� �x�����E���̉����C���s�[�_���X�͂Q�D�R�X�~107�����^���Q�^����,���̉����C���s�[�_���X1.41�~10�U�����^���Q�^�����P�V�{�傫�������Ē���g�ł��e�����Ɛ��Ƃ̕����l���������蔽�˂���������B �Q�l ���Ƃ��āC�x�����E�������a����0.23���i����1.44���j�Ƃ����,������1�̈ꎟ���U�s�[�N�Ŏ��g����976�g���ƂȂ�C���U�ł̎��g����,�Q.15���g���ƂȂ�B�^�[�Q�b�g����̊��S���˂悤�Ƃ����,
2.15���g�����x�̎��g���ʼn��g��łK�v������ |
||
|
�}���@�Z��Ήp���̔��ˌW�� |
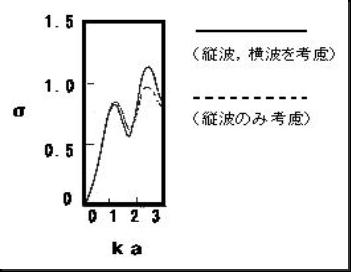
�c�g�Ɖ��g���l�������v�Z���� �x�����E���Ǝ����悤�Ȕ��ˌW����������������P�Ŕ��ˌW���̈�Ԗڂ̋��U�s�[�N������顃Ё�0.5�Ńx�����E���̈ꎟ���U���x���Ƃقړ����ł���B������2.�P�ő��̋��U���N����Ё�1.�R�T�ł��顃x�����E���ɔ�ׂĔ��ˌW���́C���傫���B �c�g�݂̂��l�������v�Z���� �������P�Ŕ��ˌW���̈�Ԗڂ̋��U�s�[�N������顏c�g�Ɖ��g���l�������ꍇ�Ɠ������Ё�0.5�ł��額X�ɏc�g�Ɖ��g���l�������ꍇ���c�g�̂ݍl�������ꍇ��,���ˌW���͂�����1.8�ȉ��͈̔͂łقƂ�Ǔ����ł��顂��͈̔͂ł͉��g�̉e�����Ȃ����Ƃ����顈��,������1.8�ȏ�ł�,�c�g�Ɖ��g���l�������ꍇ�ɔ�ׂč����傫������ˌW���̑��̃s�[�N�͍��X�Ё�0.7�Ə������B �����C���s�[�_���X�ɂ�錟���Z��Ήp���̉����C���s�[�_���X�͂P�D�R�P�~107�����^���Q�^����,���̉����C���s�[�_���X1.41�~10�U�����^���Q�^�����P�W�D�T�{�傫����Z��Ήp�Ɛ��̕����l�̍��́C�x�����E���Ɛ��̕����n�̍��Ƃ��܂�ς��Ȃ��C������1.8�ȏ�ł͉��g���Z��Ήp���̏c�g�U���ɃJ�b�v�����O���傫�ȐU��������ƍl������B |
||
|
�}���@�S���̔��ˌW�� |
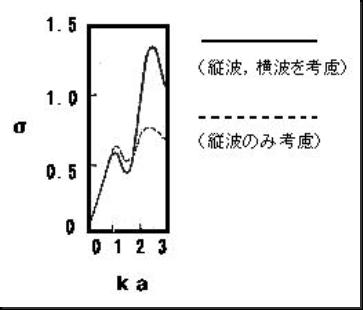
�c�g�Ɖ��g���l�������v�Z���� �x�����E����Z��Ήp�ƈقȂ锽�ˌW����������������P�Ŕ��ˌW���̈�Ԗڂ̋��U�s�[�N������顂������Z��Ήp��蔽�ˌW���͑傫���Ё�0.�W�ł��顈��������2.�R�ő��̋��U���N���邪�Ё�1.�P�T�ŗZ��Ήp�̏ꍇ��菬�����B �c�g�݂̂��l�������v�Z���� �������P�Ŕ��ˌW���̈�Ԗڂ̋��U�s�[�N������顏c�g�Ɖ��g���l�������ꍇ�Ɠ������Ё�0.�W�ł��額X�ɏc�g�Ɖ��g���l�������ꍇ���c�g�̂ݍl�������ꍇ��,���ˌW���͂������Q�ȉ��͈̔͂łقƂ�Ǔ����ł��顂��͈̔͂ł͉��g�̉e�����Ȃ�����,�������Q�ȏ�ł�,�c�g�Ɖ��g���l�������ꍇ�ƍ�������������ˌW���̑��̃s�[�N�͂قڊ��S���˂ŃЁ��P�ł���B �����C���s�[�_���X�ɂ�錟�� �S�̉����C���s�[�_���X�͂S�D�T�X�~107�����^���Q�^����,���̉����C���s�[�_���X1.41�~10�U�����^���Q�^�����R�Q�D�U�{�傫����S�Ɛ��̕����l�̍��́C�x�����E����Z��Ήp�̏ꍇ�ɔ�ׂĂ͂邩�ɑ傫���C�}�̂悤�ɓS���ł́C�x�����E����Z��Ήp�����Ⴂ���g������傫�Ȕ��˂�������B�܂��������R�ȉ��͈̔͂ŁC���g���S���̐U���ɃJ�b�v�����O���e���͏��Ȃ��ƍl������B |
||
|
�}���@�A���~�j�E�����̔��ˌW�� |
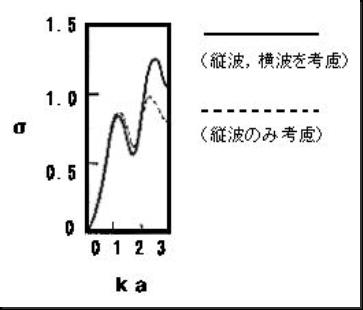
�c�g�Ɖ��g���l�������v�Z���� �Z��Ήp�Ƃ悭�������ˌW���������B�������P�Ŕ��ˌW���̈�Ԗڂ̋��U�s�[�N������顂��̒l�Ђ�0.�U�ŁC�x�����E����Z��Ήp�̈ꎟ���U�s�[�N��菭���傫���B������2.�Q�ő��̋��U���N����Ё�1.�R�T�ł��顗Z��Ήp�Ƃقړ����ł���B �c�g�݂̂��l�������v�Z���� �������P�Ŕ��ˌW���̈�Ԗڂ̋��U�s�[�N������顏c�g�Ɖ��g���l�������ꍇ�Ɠ������Ё�0.�U�ł��額X�ɏc�g�Ɖ��g���l�������ꍇ���c�g�̂ݍl�������ꍇ��,���ˌW���͂�����1.8�ȉ��͈̔͂łقƂ�Ǔ����ł��顂��͈̔͂ł͉��g�̉e�����Ȃ�����,������1.8�ȏ�ł�,�c�g�Ɖ��g���l�������ꍇ�ɔ�ׂč����傫������ˌW���̑��̃s�[�N�͍��X�Ё�0.7�ł���B �����C���s�[�_���X�ɂ�錟�� �A���~�j�E���̉����C���s�[�_���X��1.73�~107�����^���Q�^����,���̉����C���s�[�_���X1.41�~10�U�����^���Q�^�����12.3�{�傫���������1.8�ȏ�ł͉��g���A���~�j�E�����̏c�g�U���ɃJ�b�v�����O���傫�ȐU��������ƍl������B |
||
|
�}���@�^�J���̔��ˌW�� |
�c�g�Ɖ��g���l�������v�Z���� �S�Ƃ悭�������ˌW����������������P�Ŕ��ˌW���̈�Ԗڂ̋��U�s�[�N������顓S�Ƒ�̓����Ŕ��ˌW���̓Ё�0.�W�ł��顈��������2.�R�ő��̋��U����������B�������S���͑傫�����U���x���������Ё�1.�Q�T�ł���B �c�g�݂̂��l�������v�Z���� �������P�Ŕ��ˌW���̈�Ԗڂ̋��U�s�[�N������顂��̃s�[�N�̒l�́C�c�g�Ɖ��g���l�������ꍇ�Ɠ������Ё�0.�W�ł��額X�ɏc�g�Ɖ��g���l�������ꍇ���c�g�̂ݍl�������ꍇ��,���ˌW���́C�������Q�ȉ��͈̔͂łقƂ�Ǔ����ł��顂��͈̔͂ł͉��g�̉e�����Ȃ�����,�������Q�ȏ�ł�,�c�g�Ɖ��g���l�������ꍇ�ƍ�������������ˌW���̑��̃s�[�N�͂قڊ��S���˂ŃЁ��P�ł���B �����C���s�[�_���X�ɂ�錟�� �����C���s�[�_���X���x��4.04�~107�����^���Q�^���Ő��̉����C���s�[�_���X���x�P�D�S�P�~�P�O�U�����^���Q�^�����,28.7�{�傫����^�J���ł́C�x�����E����Z��Ήp��A���~�j�E���������Ⴂ���g���ő傫�Ȕ��˂�������B���̓_�œS���Ɣ��ɗǂ����Ă���B�܂��������R�ȉ��͈̔͂ŁC���g���^�J���̏c�g�U���ɃJ�b�v�����O����e���͏��Ȃ��ƍl������B |
||
|
�@ �}���@���[�T�C�g���̔��ˌW�� |
�c�g�Ɖ��g���l�������v�Z���� �x�����E�����C�Z��Ήp���C�S���C�A���~�j�E�����C�^�J���̂�����Ƃ��قȂ锽�ˌW���������B�������P.�R�Ŕ��ˌW���̈�Ԗڂ̋��U�s�[�N������顃Ё��U.�W��,����߂č������˂�������B������2.�P�ő��̋��U���N����Ё��U��,������傫�����˂������B�������U�ɂ����Ă���Ԗڂ͂������P.�X�ŃЁ��Q.�P,��Ԗڂ͂������Q.�T�ŃЁ��P.�W�Ɗ��S���˂�傫�������Ă��邱�Ƃ�����B����������P�ȉ��ɂ����Ă͋ɂ߂Ĕ��ˌW�����������B �c�g�݂̂��l�������v�Z���� ���U�s�[�N�͌���Ă��Ȃ��B���ˌW���͂����̑���ɑ��Ċ��炩�ɕω����ő�ł��O.�R���炢�ł���B�������P�ȉ��͈̔͂ł́C�c�g�Ɖ��g���l�������ꍇ�Ɠ��������Ȕ��ˌW����������v���Ă���B�������P�ȉ��͈̔͂�,���ˌW���͉��g�̉e�����Ȃ����Ƃ���������C������1�ȏ�ł͉��g�����[�T�C�g���̏c�g�U���ɃJ�b�v�����O���傫�ȐU��������ƍl������B �����C���s�[�_���X�ɂ�錟�� ���[�T�C�g���̉����C���s�[�_���X�́C�R�D�P�U�~�P�O�U�����^���Q�^���ł���C���̉����C���s�[�_���X�P�D�S�P�~�P�O�U�����^���Q�^���̍��X�Q�D�Q�{�ł���B�������P�ȉ��ŏ��������ˌW���������̂́C���[�T�C�g���̉����C���s�[�_���X������̐��Ƌ߂��l�ł���C���g�̑啔�������������܂���������[�T�C�g�������ւƓ��߂��邽�߂ł���B���߂���g��������Δ��˂���g�͏��Ȃ��B |
||
�}���@��C���̔��ˌW�� |
�v�Z���� �x�����E�����C�Z��Ήp���C�S���C�A���~�j�E�����C�^�J�����[�T�C�g���̂�����Ƃ��قȂ锽�ˌW���������B���ˌW���̋��U�s�[�N�͂������������Ƃ���ɔ������C�����̑���Ɣ��ɂȂ��炩�Ɍ������P�ɋ߂Â��B���������ċ�C�̏ꍇ�͂قڊ��S���ˑ̂ł���B �����C���s�[�_���X�ɂ�錟�� ��C�̉����C���s�[�_���X�́C�S�D�O�W�~�P�O�Q�����^���Q�^���ŁC���̉����C���s�[�_���X�P�D�S�P�~�P�O�U�����^���Q�^���ɔ�ׂĂ͂邩�ɏ������B���̂悤�ɉ����C���s�[�_���X�̓_�������C���́C����̐��ƑS�R�قȂ�B����ĉ��g��ǂ����˂���B |
||
|
�܂Ƃ� �����C���s�[�_���X�̑傫���S��^�J�ł́C�������ˌW���������B�ގ��̖��x���傫���̂���̗��R�ł���B���ʼn����C���s�[�_���X�̑傫���x�����E���C�Z��Ήp�C�A���~�j�E���Ȃǂ̃O���[�v�ł́C����g�œS��^�J�̂U�����x�̔��ˌW�����������C�����g�ɂ����ēS��^�J��荂�����ˌW���������B���[�T�C�g�ł͒���g�ɂ����ĂقƂ�lj��g���߂����ˌW�����������B��C�ł͉����C���s�[�_���X���ɂ߂ď��������߁C����g����傫�����ˌW���������B�S��^�J�ł́C�����g�ł��C�قƂ�Ǐc�g�̐U����͂Ŕ��ˌW�������߂��邪�C�x�����E���C�Z��Ήp�C�A���~�j�E���Ȃǂ̃O���[�v�ł͉��g�̉e�����傫���o��B���̌��ʍ������ˌW���������B |
|||
|
�Q�l����: |
|
R.Hickling;
�gAnalysis of Echoes from a Solid Elastic Sphere in Water,�h
J.Acoust.Soc.Am.vol.34,no.10,pp1582-1592,(1962) |
|
|
|