Analysis of sound field generated by a low frequency sound source

in a　water tank surrounded by infinite ground

1.Introduction

      Recently, the needs of low frequency sound source to  be applied for oceanography observation or sea bottom exploration are increasing. To recognize the large structure like the ocean or earth,　low frequency sound source is regarded as useful one.　The reason is that the wave emanated by that has least loss, in the propagation process. Therefore, such a low frequency sound source that generates sound signal with stability and large power becomes important.  As a trial, an underwater oil pressure drive low frequency sound source  was designed for these needs. Then, to check how it generates high pressure level, in a water tank,  an experiment was carried out.  In general, in the tank, sound level is not always obtained by the reason of echo. However, it is not evident whether the echo affects the nearest area of the sound source, or not. In this paper, in order to investigate the influence of an echo within the tank, sound pressure to be generated by a  low frequency  sound source  is  evaluated by the theoretical method. Moreover, the comparisons of theoretical data and experiment are also carried out.

In case solving problem such as sound waves in water,  sound  field  is determined by using analytical method, because tank wall and ground are correlated each other.  For an example, as analytical methods,  Ritz Method^1),2) Galerkin Method^3),4)and Mode Matching Method^5)-8) are applied, by using power series. These features have advantage as follows, 1) The diffraction phenomena of the sound  field can be strictly taken into account if that power series satisfies the wave equation.  2) Convergence is good and high-speed calculation is performed. In this paper, a new method is proposed into which Mode Matching Method is expanded.

２．Theoretical Analysis

２．１　Formulation of sound  fields

Since we are discussing about low frequency in this analysis, only a sound wave (standing wave)   is taken into consideration,  disregarding  traverse wave  among  elastic wave, in every regions. Besides, internal loss contained in the ground is neglected. As an analytical model, the tank placed under the infinite ground is shown in Fig.1. A rectangular coordinates system(X, Y, Z) whose origin is set at the center of rectangular tank surface,  is defined. Plus direction of Z-axis is defined to downward vertically. Sound source is a cylindrical type whose ends  have discs  vibrating symmetrically.However, in this paper, two pulsating point sound sources with same volume velocity  as the disc are placed on each disc center.  If the enclosure is constructed by hard materials  and that  scale is  smaller compared to the wave length of interest, this might be reasonable⁹⁾.

 　　As shown in Figure.1, the point source position is defined as（ｘ_ｑ，ｙ_ｑ，ｚ_ｑ）.  The vector from origin to the point q is defined as　Ｒ_ｑ. The elements of Ｒ_ｑis defined as（Ｒ_ｑ，θ_ｑ，φ_ｑ）by using polar coordinate system or as（ｒ_ｑ，ｚ_ｑ，φ_ｑ）by cylindrical coordinate system. The vector indicate arbitrary point  in  the water is defined as Ｒ_Ｗ,,  the  vector indicates arbitrary point inside the tank wall is defined as　Ｒ_Ｖ, on the extended line  where　Ｒ_Ｗis  included, and the vector indicates arbitrary point in the ground is defined as　Ｒ_Ｕ.　In addition, the  elements of vector　Ｒ_Ｗ，Ｒ_Ｖ，Ｒ_Ｕ　are defined as（Ｒ_Ｗ，θ，φ），（Ｒ_Ｖ，θ，φ），（Ｒ_Ｕ，θ，φ）by polar coordinate system, and as（ｒ_Ｗ，ｚ_Ｗ，φ），（ｒ_Ｖ，ｚ_Ｖ，φ），（ｒ_Ｕ，ｚ_Ｕ，φ）by cylindrical coordinate system.  The argument between　Ｒ_ｑand　Ｒ_Ｗ　is defined asΘ_ｑＷ,　and  unit vectors in X ,Y and Z are defined as　ｅ₁，ｅ₂，andｅ₃respectively.     

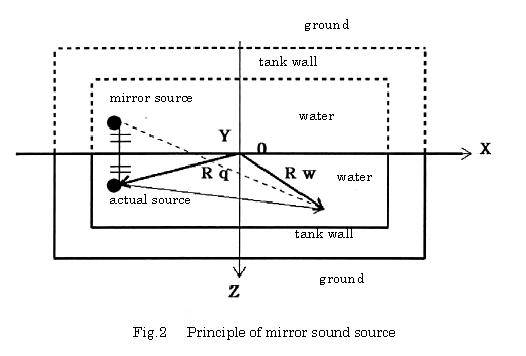
 　　 Sound  field in the water is determined by considering continuity of both sound  pressure  and normal particle velocity at the boundary of water, tank wall, and ground , and that free pressure condition as to surface of water, tank wall, and ground .  If the later condition is applied to this problem directly,　however, the condition: free pressure  has to be incorporated in the whole.  In this case,  it causes  increase in time  and  memory in calculation.

On the other hand, it is known that sound  field can be solved  by using mirror image principles¹⁰⁾ .  So, this method is applied to solve the present problem. That principle is shown in Fig.2. A dashed line indicates such the state that both water tank and  ground  were  reversed vertically. In this configuration, two  sound sources are placed. A source inside the solid line is called as actual sound source and another source inside the dashed line is called as mirror source or virtual sound source.  Such  two sound sources are 180 degree different  in phase  but have same amplitude and  are placed symmetrically to XY plane.  Where Y axis  is defined  positive to the front perpendicularly.

Consequently, if these sounds are superimposed, the field which satisfies surface boundary  condition will be obtained.    

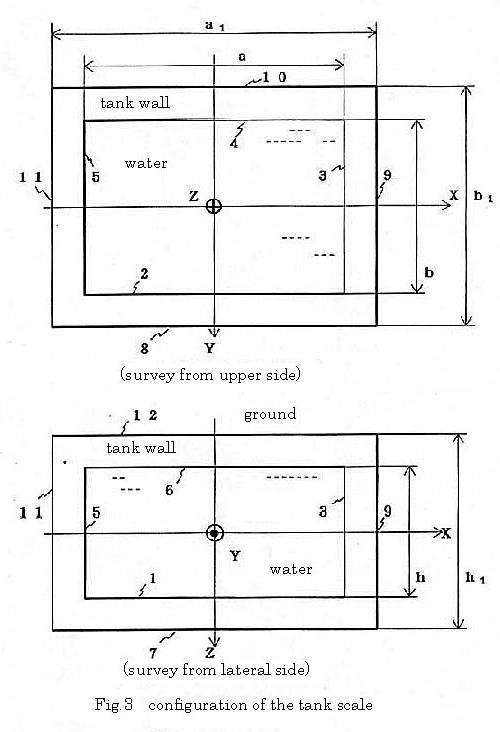
As shown in Fig.3,　the boundary between water  and tank wall  is  divided  from  region 1 to region 6,and the boundary between tank wall and ground is divided from  region 7 to region 12. The coordinates of the arbitrary points on region i are defined as（R_i，θ_i，φ_i）by polar coordinate system，and as（ｒ_i，ｚ_i，φ_i）by cylindrical coordinate system.  In the arbitrary point W in the water , the velocity potential Φ_ｑgenerated  by the spherical wave with volume velocity Ｑ_ｑemanated from point q is given as follows;

where, k is wave number in the water and is expressed by ω/C,（ω：circular frequency，C:sound  speed in

water）,and the time function expressed as exp(jωｔ) was omitted.

Moreover, since Eq.(1)  satisfies radiation condition ,in the infinite field,  it is  expressed as power series using polar coordinates variables as follows,

where,ｊ_ｎ，h_ｎ^（２），and P_ｎare  the first kind spherical Bessel function of nth order,　the second kind  spherical Hankel function of nth order, and the first kind Legendre function of  nth order, respectively. R＜means min（R_Ｗ，R_ｑ）and R＞ mean max（R_Ｗ，R_ｑ）. In Eq.(2), P_ｎ (cosΘ_ｑＷ)  is  expressed  by the additional theorem .re. Legendre function,

Then, in substitution of Eq. (3) into Eq. (2),

where，

On the other hand,  at point W ,  the velocity potential  Φr of  wave  reflected   from the tank wall is expressed by power series as follows, 

where,

Ψ_ｎｍ^r(R_Ｗ)=ｊ_ｎ(kR_Ｗ)P_ｎ^｜ｍ｜(cosθ)exp(jmφ)　　　　　　　　　　　　　　　　（５）

A_nm^ｑis a unknown constant to be determined by the boundary conditions. The velocity  potential of wave refracted in the tank wall  is defined as Φ_T.,,

Φ_T is also expressed below, by power series,

where,

Λ_ｎｍ(R_Ｖ)=j_ｎ(k_ＴR_Ｖ)P_ｎ^｜ｍ｜(cosθ)exp(jｍφ)

Υ_ｎｍ(R_Ｖ)=n_ｎ(k_ＴR_Ｖ)P_ｎ^｜ｍ｜(cosθ)exp(jｍφ)　　　　　　　　　　　　　　　（６）

where,n_ｎmeans the second kind spherical Bessel function of nth oder, k_Ｔmeans the wave number in the tank wall ,and is given as k_Ｔ=ω/c_Ｔ by using c_Ｔ  (sound speed in the tank wall),and ω ( circular frequency). B_nm^ｑ,and C_nm^ｑare also unknown constants to be determined by the boundary conditions.

The velocity potential of wave which penetrates into ground from the tank wall is defined as Φ_Ｄ at the point u. Φ_Ｄ is given as follows, by using power series, since Φ_Ｄ  has to satisfy radiation condition in infinite field.

where，

Ψ_ｎｍ^Ｄ(R_Ｕ)=h_ｎ^（２）(k_ＤR_Ｕ)P_ｎ^｜ｍ｜(cosθ)exp(jmφ)　　　　　　　　　　　　　　　　　　　　（７）

D_nm^ｑis also unknown constant determined by boundary conditions.

２．２　Determination of unknown constants

Unknown constants  A_ｎｍ^ｑ，B_ｎｍ^ｑ,　C_ｎｍ^ｑ, and  D_ｎｍ^ｑ, are determined  by  the  following boundary conditions. With respect to the normal particle velocity of region i, (where, i=1 ,.., 6)　sum total of incident wave and reflected wave is equal to refracted wave which is generated in the tank wall.

－ｎ∇Φ_ｑ｜_RＷ＝Si－ｎ∇Φ_ｒ|_RＷ=Si=－ｎ∇Φ_Ｔ｜_RＶ＝Si　　　　　　　　　　　　（８）

where，ｎis unit vector normal to the surface of region. Ｓｉis the vector positioning the surface of region i. ｎ∇is a calculus operator to obtain a differential coefficient with respect to normal direction of the regional surface, and then,

ｎ∇=(ｎ_xｅ₁+ｎ_yｅ_２+ｎ_zｅ₃)･(ｅ₁∂/∂x+ｅ₂∂/∂y＋ｅ₃∂/∂z)　　　　　　　　（９）

where，ｎ_x,ｎ_y, and ｎ_z are elements of unit vector ｎ as to the direction X, Y, and Z respectively.　 Incident pressure from water to tank wall is defined as P_ｑ,reflective pressure from tank wall to water is defined as P_ｒ,and refractive pressure into tank wall is defined as P_Ｔ. Hence, sum total of incident and reflective pressure is equal to refractive pressure,

P_ｑ|_RＷ=Sｉ＋P_ｒ|_Rｗ=Sｉ=P_Ｔ|_RＶ=Sｉ　　　　　　　　　　　　　　　　　　　　　　(10)

At region i,(where, i=7,..,12) , on the other hand, since normal particle velocity of scattered wave into ground is equal to that of refracted wave into tank wall,

－ｎ∇Φ_Ｔ|_{ＲＶ＝Ｓｉ}＝－ｎ∇Φ_Ｄ|_{ＲＤ＝Ｓｉ}　　　　　　　　　　　　　　　　　　（11）

The pressure of wave refracted from tank wall to ground is defined as P_Ｄ. Since  the pressure  of scattered wave into ground is equal to that of refracted wave in the tank wall,

P_Ｔ|_RＶ=Si＝P_Ｄ|_RＵ＝Si　　　　　　　　　　　　　　　　　　　　　　　　　（12）

Unknown constants ,however, are never obtained strictly , except  for  such a  simple  form like a sphere.

For this problem, on the other hand, a method obtaining unknown constants by assuming wave mode of structure has been suggested. That is least mean square method,  and is called as  Mode Matching Method. This is  a  useful method ,but is difficult to apply for such boundary value problem of the present tank whose surroundings are layered with different mediums, because  the values of pressure  or particle  velocity of each boundary cannot be known.

Such problem is often called as sound correlation problem.  Here, to determine unknown constants, a new method，Mode Matching Method Expansion ,is proposed.

２．３　Application of mode matching method expansion

In each Eq.(8), Eq.(10), Eq.(11),and Eq.(12), the absolute of  value  subtracting the right hand side from left hand side , are defined as ε₁，ε₂, ε₃，and ε₄　 respectively,

ε₁=｜-ｎ∇Φ_ｑ｜_RＶ=Si　-ｎ∇Φ_ｒ｜_RＷ=Si　+ｎ∇Φ_Ｔ｜_RＶ=Si|　　　　　　　　（13）

ε₂=｜P_ｑ｜_RＷ=Si＋P_r|_RＷ=Si-P_Ｔ｜_RＶ=Si｜　　　　　　　　　　　　　　　　（14）

ε₃=｜-ｎ∇Φ_Ｔ｜_RＶ=Si＋ｎ∇Φ_Ｄ｜_RＤ＝Si｜　　　　　　　　　　　　　　　（15）

ε₄=|P_Ｔ|_RＶ=Si-P_Ｄ|_RＵ＝Si|　　　　　　　　　　　　　　　　　　　　　（16）

where,ε_１，ε_２，ε_３，andε₄， should be 0.

However,as shown in Fig.3, the boundary shapes with respect to region1, region2… and  region12  are not adapted with coordinate system expressed by spherical coordinate. So all these values have errors. Thus,  unknown constants A_ｎｍ^ｑ，B_ｎｍ^ｑ，C_ｎｍ^ｑ，and D_ｎｍ^ｑ are determined ,by minimizing the sum of squared errors E ofε_１，ε_２，ε_３and ε_４in entire region .These error E are given below,

E  =

_４

Σ

∫∫

ε_j^２ｄｓ

^ｊ＝１

=

_６

Σ

∫∫

|-ｎ∇Φ_ｑ-ｎ∇Φr+ｎ∇Φ_Ｔ|^２ｄsi

^ｉ=1

_６

     ＋Σ

∫∫

｜ｊωρΦ_ｑ＋ｊωρΦr－ｊωρ_ＴΦ_Ｔ|^２dsi

^ｉ＝１

            _１２

＋Σ

∫∫

|-ｎ∇Φ_Ｔ+ｎ∇Φ_Ｄ|^２dsi

               ^ｉ=7

            _１２

     ＋Σ

∫∫

｜ｊωρ_ＴΦ_Ｔ-ｊωρ_ＤΦ_Ｄ|^２dsi　　　(17)

              ^ｉ=7

where, * means complex conjugate. In Eq.(18) to which Eq.(4)，Eq.(5)，Eq.(6),and Eq.(7)are substituted, the value of E is found not to be related with unknown constants A_ｎ’ｍ’^ｑ＊，Ｂ_ｎ’ｍ’^ｑ＊，Ｃ_ｎ’ｍ’^ｑ＊，Ｄ_ｎ’ｍ’^ｑ＊. If partial differentiation ∂Ｅ’/∂A_ｎ’ｍ’^ｑ＊，∂E’/∂B_ｎ’ｍ’^ｑ＊＝０, ∂E’/∂C_ｎ’ｍ’^ｑ＊＝０　，and ∂E’/∂D_ｎ’ｍ’^ｑ＊＝０ are applied, then the matrix equation about A_ｎ’ｍ’^ｑ＊,B_ｎ’ｍ’^ｑ＊，C_ｎ‘ｍ’^ｑ＊，D_ｎ’ｍ’^ｑ＊is obtained.

However, the formulated matrix element representation is omitted on account of screen limitation here.

After solving the matrix equation, the value Anmｑ is obtained. In substitution of this value to Eq. (5), the velocity potential of the scattered wave generated in the tank is obtained. Then, summing this to that of the emanated wave expressed as Eq.(4), vector potential Φr is obtained.

Consequently, summing the vector potential generated by a virtual sound source to that, we can obtain velocity potential generated in the tank whose upper boundary faced air. By the vector potential theorem, pressure P is expressed below,

where, N means the number of truncation terms of power series.

3.  Numerical examples and experimental results

The outside of the tank wall is covered with sand ,and that outside is covered with ordinary soil. However,　in calculation,　outside of the tank wall were all assumed to be covered with sand.  The  tank wall is constructed by concrete. The density and sound speed in sand were selected by the references ¹²⁾, and the density and sound speed in tank wall were selected by the references ^{13), 14)}. Parameters for calculation are shown in Table.1.  In Table.1, the scale of tank is equal to that of piled tanks vertically.

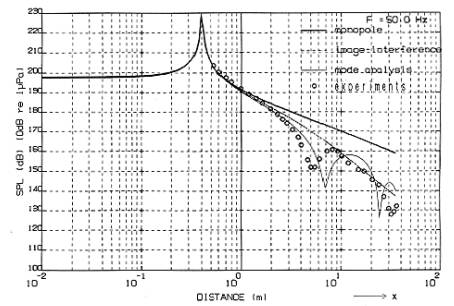
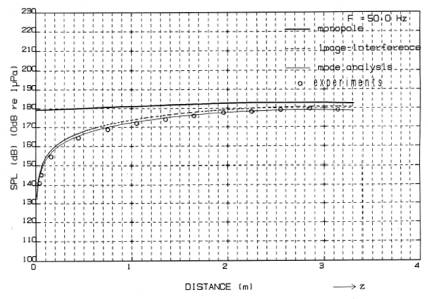
In Fig.4,the sound pressure generated at Y=0 ，Z=2．63m　,in the direction paralleled to X axis is shown. That direction is on the line of the cylinder axis of the sound source ,so is called as “sound axis”.

For comparison, four kind of data are shown in Fig.4.'monopole' is the sound pressure of  infinite free field (see Fig.1), 'image interference' is the sound pressure of semi-infinite water field whose  upper  side is air ,'mode analysis' is sound pressure in the tank where both reflection and transparency are considered. And 'experiment' is the experimental result.　From Fig.4, 'monopole', 'image interference',  and 'mode analysis'  show  the almost same results within 1dB in the range of 1m .

On the other hand, in the range beyond 1m, both 'image interference' and 'Mode analyses' that are affected by the water surface reflection become lower than 'monopole'.  In addition,  'mode  analysis' is extremely lower than 'monopole' or 'image interference' in  the far  field  about  7m  or  25m.　In  comparison 'experiments' with 'mode analysis', they are almost alike within the distance of 3m.  Beyond  3m, the distance where sound pressure becomes minimum is nearly 7m or 25m in 'mode analysis' ，while nearly 5.5m or 30m in 'experiments'.

The reason of this discrepancy is as follows; 1) In calculation, a wave function  without  considering  the internal loss factor 15), in the sandy region. 2) As actual water tank is constructed by the concrete material in which some steel ribs are inserted, and the wall thickness of water tank is not constant. 3) The parameter values re concrete or ground used in calculation differ from actual data.

Fig4 sound pressure generated at X (Y=0,Z=2.63m)

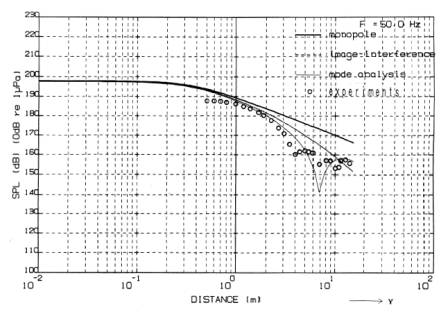
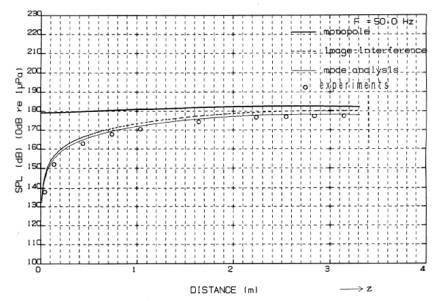
From these results, sound pressure downed in the distance near  both 7m  and  25m seems caused by the reflection from wall of the water tank. 　The sound pressure generated in the direction Y (X=0,Z=2.63m) is shown in Fig.5. In this figure, 'image　interference'，'mode　analysis', and 'experiments'  are  found  to be lower than 'monopole' . In the range, Y>1m and Y<3m, the 'experiments' is almost alike the 'mode　analysis'. However, inside the distance of 1m,'experiments' indicate lower than 'mode　analysis', for example, 5dB  lower in the distance of 0.6m.This difference seems caused by reflection loss of air inside the cylindrical enclosure of sound source.

Hence,  it  was concluded  that sound  pressure obtained by the experiments was almost same to that of 'monopole', within 1m re sound axis.  To  the contrary, outside 1m in both sound axis direction and the direction perpendicular to the acoustic axis, such sound pressure representative to the 'monopole' was not obtained owing to reflection from both water surface and water tank wall.

Fig.5　sound  pressure generated in the direction Y (X=0,Z=2.63m)

The sound pressure generated in the direction Z (X=2.3m,Z=0) is shown in Fig.6.  'experiments'  is  lower than 'monopole'. 'experiments' is close to 'monopole' at the deep position in the tank.  This is the reason that water surface reflection scarcely affects to 'monopole' at the deep position.

However, other sound pressures except for 'monopole' are 2dB lower than 'monopole'. So ,　in such water tank as depth is 3.2m , the water surface reflection seems affective to 'monopole'.

Fig.6   sound pressure generated in the direction Z (X=2.3m,Z=0)

The　value of　the generating sound pressure of the Z-axis direction containing X= 0 and Y= 2.3m is shown in Fig. 7. 'experiments' is lower than 'monopole'. Moreover, 'mode analysis' , 'image interference' ,and 'experiments' are almost same.　　　

From these results, the free field sound pressure is found to be equal with experimental data ,at less than 1.5m along Z-axis directions of the tank.   However,  the  region  within 1m in which sound pressure is not in inverse proportion to the distance is near field . Thus, sound  pressure  in  the far field  cannot  be converted from this measured value.

     On the other hand, as for 'mode analysis' proposed here, the sound field considering reflection of surface and tank wall can be calculated.　Then in the further distance than 5m,'mode analysis' was  found mostly suited to the experimental results. So, this proposed technique seems useful to the sound field prediction within the echoic tank.　　　　

Fig.7 sound pressure generated in the direction Z (X=0,Y=2.3m)

４．Conclusions

In a water tank surrounded by the infinite ground, a sound field generated by the  two-point  sources as a model of low frequency sound source of cylindrical type of which ends have discs　was calculated  by the Mode Matching Method Expansions, and was compared to the experimental results.　Moreover, free field sound pressure generated by monopole source, and semi free field sound pressure generated by method of 'image-interference' were calculated .and were compared to the experimental results.　

As conclusion, the error between experimental results and mode analysis results was found large near the sound source enclosure surface about a direction perpendicular to the sound source axis. This is considered to be the influence of reflection of the air inside the enclosure. Taking the enclosure shape into consideration in calculation will be tried to prove this discrepancy in the future.

References

1）R.Woodcock　and　J.Nicolas, “A　generalized　model　for　predicting the sound transmission properties

 　of generally orthotropic plates with arbitrary boundary conditions,” J.Acoust.Soc.Am.97(2),ｐ1099-1112,(1995)

2)K.m.Liew.C.W.Lim.”Vibratory Characteristic trapezoids,” J.Sound Vib.183(4),ｐ615-642,(1995)

3)P.A.A.Laura an R.Gutierrez,”Fundamental frequency of vibration of clamped plates of arbitrary shape

subjected to a hydro-static state of in-plane stresses,”

4) M.Okajima, C.B.Burroughs, and J.P.Charpie,”An analytic model for the frequencies of resonance of rectangular

plates of variable curvature and thickness,” J.Acoust .Soc.Am.97(2),ｐ1053-1060.(1995)

5)H.Ikuno and K.Yasuura,”numerical calculation of scattered field from a periodic deformed cylinder using the smoothing process on the mode matching method,”Radio Sci.13.ｐ937-946,(1978)

6) W.Williams.et al.,”Acoustic radiation from a finite cylinder,”J.acoust.Soc.Am.36 (12), 2316-2322, (1964)

7)H.Suzuki,J.Tichy,”Diffraction of sound by a convex or concave dome in an infinite baffle,” .Acoust.Soc.Am.70(5).ｐ1480-1487,(1981)

8)D.T.Diperna and T.K.Stanton,”Sound scattering by cylinders of non-circular cross section: A conformal mapping

approach,” J.acoust.Soc.Am.96.ｐ3064-3079,(1994)

9)Hayasaka　Toshio　and　Yoshikawa　shokichiro，”Onkyo　Shindoron”Maruzen CO.,Ltd.Tokyo,1974，P642,645

10)reference9),ｐ569-570

11)Moriguchi　Shigekazu,et al,”SugakukoshikiⅢ,Tokusyu　Kansu”,Iwanami　Syoten Co.,Ltd..,Tokyo,1977,P218,220

12)Motooka seiichi and Okujima Motoyoshi,”Electromagnetic Induction Type Sound Source Used for Detection of Bodies Buried in Underground”,J.Acoust.Soc..JapanVol.29 ,No.7,p403-409,(1973)

13)The National Astronomical observatory of Japan edit,”Science chronology”,Maruzen Co.,Ltd.,Tokyo,(1995)

14)Nishimaki Masao,”Denkionkyo shindo gaku”,Koronasya Co.,Ltd.,Tokyo,p47,(1978)

15) Motooka seiichi and Okujima Motoyoshi,”Measurement of Frequency Characteristics of Attenuation Constant in Sand by Impulsive Sound Wave”, J.Acoust.Soc.JapanVol.30, No.6, p325-328, (1974)