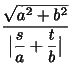作図法(1)
証明(1.1)
証明(1.2)
解説(1)
作図法(1)の手順(アニメーションのようなもの)
(作図法(1))
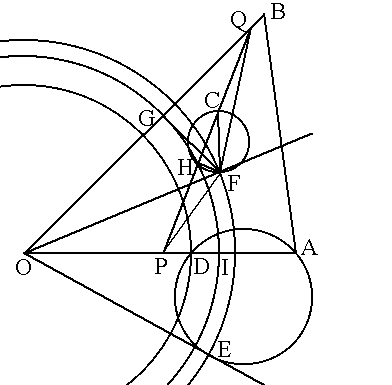 点Cを通り、三角形OABの面積を二等分する直線を作図する方法は次の通りである。
点Cを通り、三角形OABの面積を二等分する直線を作図する方法は次の通りである。
まず点Cを通りかつ線分OA,OBの両方に交わる直線が三角形OABの面積を二等分する場合を考える。
半直線OA上に
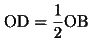 (1)
を満たすように点Dをとり、2点A,Dを通る適当な円を描く。ただし、点Oはその円の外部にあるようにする。この円の中心をJとする。線分OJを直径とする円と円Jとの交点をEとし、角AOBの二等分線上に
(1)
を満たすように点Dをとり、2点A,Dを通る適当な円を描く。ただし、点Oはその円の外部にあるようにする。この円の中心をJとする。線分OJを直径とする円と円Jとの交点をEとし、角AOBの二等分線上に
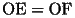 (2)
を満たすように点Fをとる。Fから直線OBに下ろした垂線の足をGとし、Oを中心としGを通る円と、CFを直径とする円との交点をHとする。直線CHは三角形OABの面積を二等分する。
(2)
を満たすように点Fをとる。Fから直線OBに下ろした垂線の足をGとし、Oを中心としGを通る円と、CFを直径とする円との交点をHとする。直線CHは三角形OABの面積を二等分する。
ただし、作図の過程でHが存在しない場合は、点Cを通りかつ線分OA,OBの両方と交わる直線で三角形OABの面積が二等分されることはない。
Hに相当するものが2個ある場合は、そのそれぞれをHとし、上の作図を2回試みるものとする。
直線CHが線分OAと交わらないまたは直線CHが線分OBと交わらない場合は、そのHからは条件を満たす直線が得られない。
同様の作図を頂点O,A,Bを読み替えて3回繰り返せば、三角形OABの面積を二等分する直線でCを通るものがすべて得られる。
(証明(1.1))
(作図により得られる直線が三角形OABの面積を二等分すること。)
直線OEが円Jの接線であるから、方べきの定理より
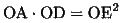 (3)
(1)(2)(3)より、
(3)
(1)(2)(3)より、
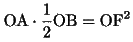
 (4)
ここで、
(4)
ここで、
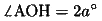 (5)
(5)
 (6)
(6)
 (7)
とする。
(7)
とする。
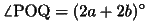 (8)
(8)
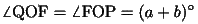 (9)
三角形OHIはOH=OIの二等辺三角形だから、
(9)
三角形OHIはOH=OIの二等辺三角形だから、
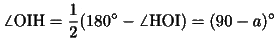 ゆえに、
ゆえに、
 (10)
同様にして、
(10)
同様にして、
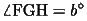 (11)
四角形HFIPにおいて、
(11)
四角形HFIPにおいて、
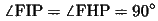 であるから、四角形HFIPは内接四角形である。したがって、
であるから、四角形HFIPは内接四角形である。したがって、
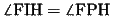 (12)
(10)(12)より、
(12)
(10)(12)より、
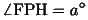 (13)
同様にして、四角形GHFQにおいて、
(13)
同様にして、四角形GHFQにおいて、
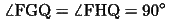 であるから、四角形HFIPは内接四角形である。したがって、
であるから、四角形HFIPは内接四角形である。したがって、
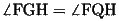 (14)
(11)(14)より、
(14)
(11)(14)より、
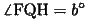 (15)
ここで、
(15)
ここで、
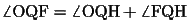 (16)
(7)(13)(16)より、
(16)
(7)(13)(16)より、
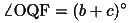 (17)
また、
(17)
また、
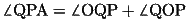 (18)
(7)(8)(18)より、
(18)
(7)(8)(18)より、
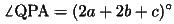 (19)
であり、
(19)
であり、
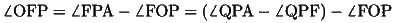 (20)
(9)(13)(19)より、
(20)
(9)(13)(19)より、
 (21)
(17)(21)より、
(21)
(17)(21)より、
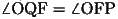 (22)
(9)(22)より、
(22)
(9)(22)より、
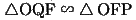 (23)
ゆえに、
(23)
ゆえに、
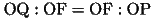
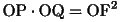 (24)
(4)(24)より、
(24)
(4)(24)より、
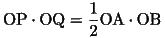 (25)
したがって、直線PQは三角形OABの面積を二等分する。
(25)
したがって、直線PQは三角形OABの面積を二等分する。
(証明(1.2))
((証明(1.1))の逆、すなわち、点Cを通る直線で線分OA、OBの両方に交わるものが作図により得られること。)
点Cを通る直線が、線分OA、OBの両方に交わるとし、その交点をそれぞれP,Qとする。さらに、
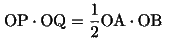 (26)
が成り立っているものとする。点D、E、F、G、I、Jは作図法のところで述べたようにとる。線分QFを直径とする円とOを中心としOGを半径とする円との交点をH'とし、直線QH'と半直線OAとの交点をP'とすると、(証明(1.1))と同様の結論がHをH'、PをP'と読み替えることにより成り立つから、
(26)
が成り立っているものとする。点D、E、F、G、I、Jは作図法のところで述べたようにとる。線分QFを直径とする円とOを中心としOGを半径とする円との交点をH'とし、直線QH'と半直線OAとの交点をP'とすると、(証明(1.1))と同様の結論がHをH'、PをP'と読み替えることにより成り立つから、
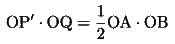 (27)
(26)(27)より、
(27)
(26)(27)より、
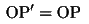 ゆえに、PとP’は一致する。したがって、P、Q、C、H'は同一直線上にあり、
ゆえに、PとP’は一致する。したがって、P、Q、C、H'は同一直線上にあり、
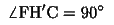 となるから、H'は作図により得られるH(のうちの一方)と一致する。
となるから、H'は作図により得られるH(のうちの一方)と一致する。
この作図法は双曲線の性質を利用しています。一般に双曲線は適当に座標軸を定めれば
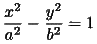 の形の方程式で表されます。この双曲線は
の形の方程式で表されます。この双曲線は
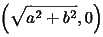 ,
, 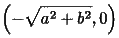 を焦点にもち、方程式
を焦点にもち、方程式
 ,
, 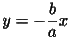 で表される直線を漸近線にもちます。
この双曲線の点T
で表される直線を漸近線にもちます。
この双曲線の点T
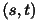 における接線の方程式は、
における接線の方程式は、
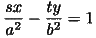 です。これと、2本の漸近線との交点は、連立方程式を解けばもとまり、結果は
です。これと、2本の漸近線との交点は、連立方程式を解けばもとまり、結果は
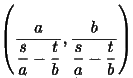 ,
, 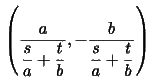 となります。これをP,Qとすると線分OP、OQの長さは、
となります。これをP,Qとすると線分OP、OQの長さは、
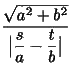 ,
, 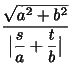 であり、2本の漸近線のなす角を
であり、2本の漸近線のなす角を
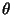 とすると、三角形OPQの面積は、
とすると、三角形OPQの面積は、
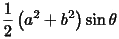 で表されることになり、これは、接点の位置にはよらない定数です。2本の漸近線のそれぞれの上に点D、Bがあるとし、
で表されることになり、これは、接点の位置にはよらない定数です。2本の漸近線のそれぞれの上に点D、Bがあるとし、
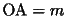 ,
, 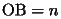 とすると、三角形ODBと三角形OMNの面積が等しくなるための条件は、
とすると、三角形ODBと三角形OMNの面積が等しくなるための条件は、
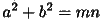 であることがわかります。すなわち、直線OD、OBを漸近線としてもち、点F
であることがわかります。すなわち、直線OD、OBを漸近線としてもち、点F
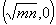 を焦点とするような双曲線を考えると、その双曲線の任意の接線と2本の漸近線とで作られる三角形の面積は
三角形ODBの面積に等しいことが分かります。このFが作図におけるFと一致します。すなわち、この作図では、まず
上でのべたような双曲線の焦点を作図しているのです。
あとは、この双曲線の接線でCを通るものが作図できればよいことになりますが、これには、双曲線の接線のある性質が
役立ちます。それは次のようなものです。
を焦点とするような双曲線を考えると、その双曲線の任意の接線と2本の漸近線とで作られる三角形の面積は
三角形ODBの面積に等しいことが分かります。このFが作図におけるFと一致します。すなわち、この作図では、まず
上でのべたような双曲線の焦点を作図しているのです。
あとは、この双曲線の接線でCを通るものが作図できればよいことになりますが、これには、双曲線の接線のある性質が
役立ちます。それは次のようなものです。
F、F'を焦点とする双曲線の点Tにおける接線は角FTF'を二等分する。
この定理を証明する問題は幾度となく大学入試で出題されています。このことこの証明は他にゆずるとして、これを
用いると、接線の作図ができることになります。
いま、
 が成り立っていてCが角FTF'の二等分線、すなわち、双曲線のTにおける接線上にあるとします。線分TF'上に
が成り立っていてCが角FTF'の二等分線、すなわち、双曲線のTにおける接線上にあるとします。線分TF'上に
 を満たすようにJをとり、線分JFと角FTF'の二等分線との交点をHとすると、
次の2つのことが分かります。
を満たすようにJをとり、線分JFと角FTF'の二等分線との交点をHとすると、
次の2つのことが分かります。
1.
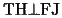 より、点Hは線分CFを直径とする円周上にある。
より、点Hは線分CFを直径とする円周上にある。
2.
双曲線の定義により、
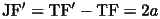 が成り立つ。さらに、Hは線分FJの中点、Oは線分FF'の中点だから、
が成り立つ。さらに、Hは線分FJの中点、Oは線分FF'の中点だから、
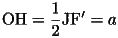 すなわち、HはOを中心とし半径がaの円周上にある。
すなわち、HはOを中心とし半径がaの円周上にある。
1.と2.より、Hはそれぞれで述べた2円の交点であることになり、作図の方法がわかりました。作図において、
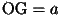 となっています。
となっています。


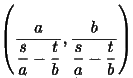 ,
, 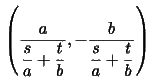
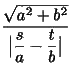 ,
,