物性 / CO₂拡散係数、物質移動係数
全体観把握目的で各種公開情報を基に作成のため、整合性が取れない場合もあります。自ら検証して御使用下さい。
全体観把握目的で各種公開情報を基に作成のため、整合性が取れない場合もあります。自ら検証して御使用下さい。
| 構成 | (1) CO₂自己拡散係数 (2) 相互拡散係数 (3) 物質移動係数 |
 溶質の濃度勾配に起因する拡散現象は、抽出・乾燥他の設計・操作に利用されます。その際、溶媒と対象物質となる抽出物資の拡散係数が物性値として必要になります。拡散現象は、次式で示されるフィック(Fick)の第一法則で表されます。
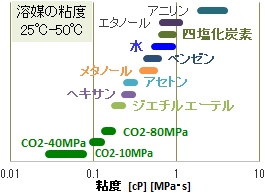
溶質の濃度勾配に起因する拡散現象は、抽出・乾燥他の設計・操作に利用されます。その際、溶媒と対象物質となる抽出物資の拡散係数が物性値として必要になります。拡散現象は、次式で示されるフィック(Fick)の第一法則で表されます。J (拡散流速) De(A,B) = R × T / { 6 × π × η(B) × r(A) } | |
 | |||
| 流体名称 | CO₂ | エタノール | 水 |
| 自己拡散係数@50℃ | 3.0E-8 @ 13MPa | 1.8E-9 | 3.7E-9 |
二酸化炭素の自己拡散係数は、通常の液体の拡散係数に比較すると、上述のように粘度が非常に小さいため、10倍~100倍大きな値になります。このため、物質の抽出、樹脂への浸透性が速くなります。
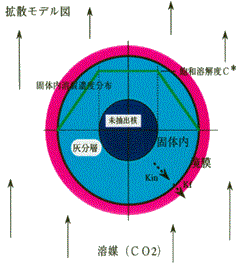
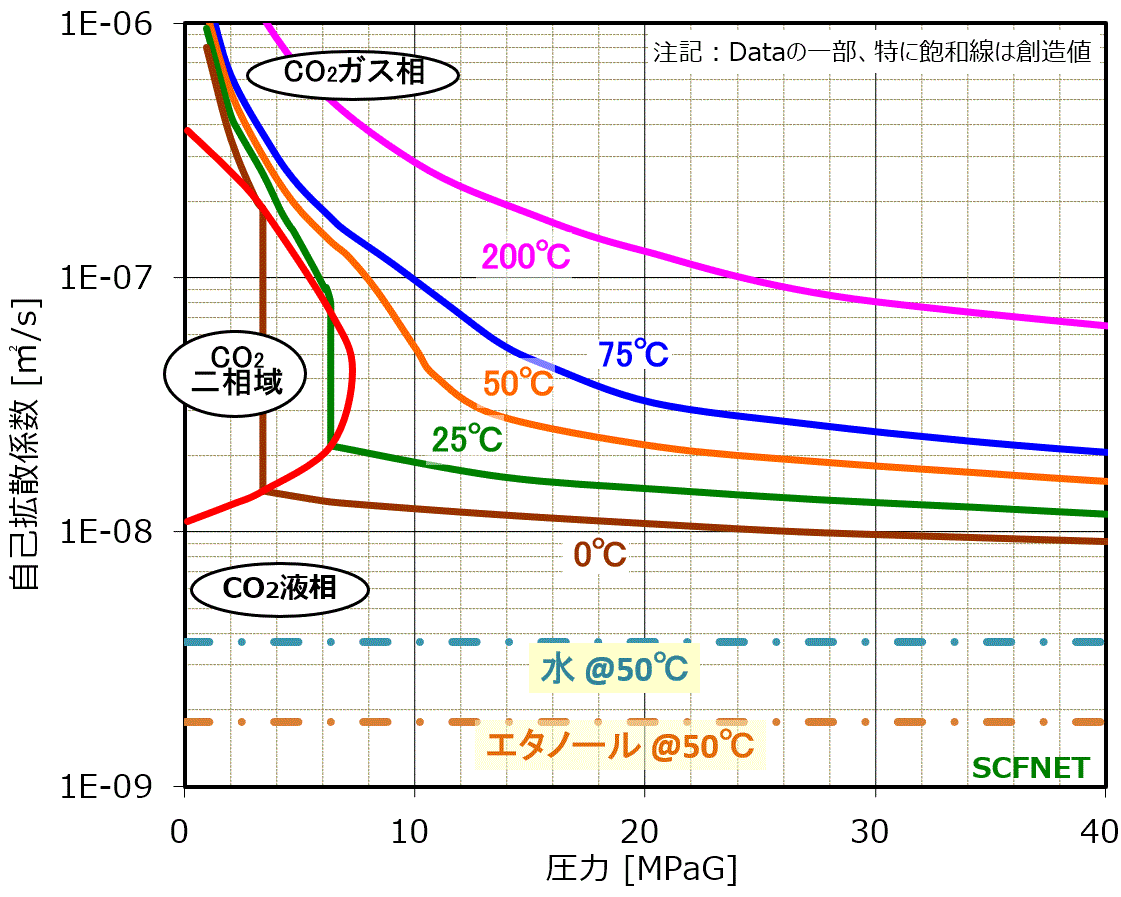
二酸化炭素の自己拡散係数のイメージ図を右図に示します。P.Etesseら、J. Chem. Phys. 97, p.2022 (1992)を基にその他の参考文献を参照してイメージ化したものです。右図に示すように、水、エタノールと比較し、一桁以上大きく、温度と圧力で大きく変化します。
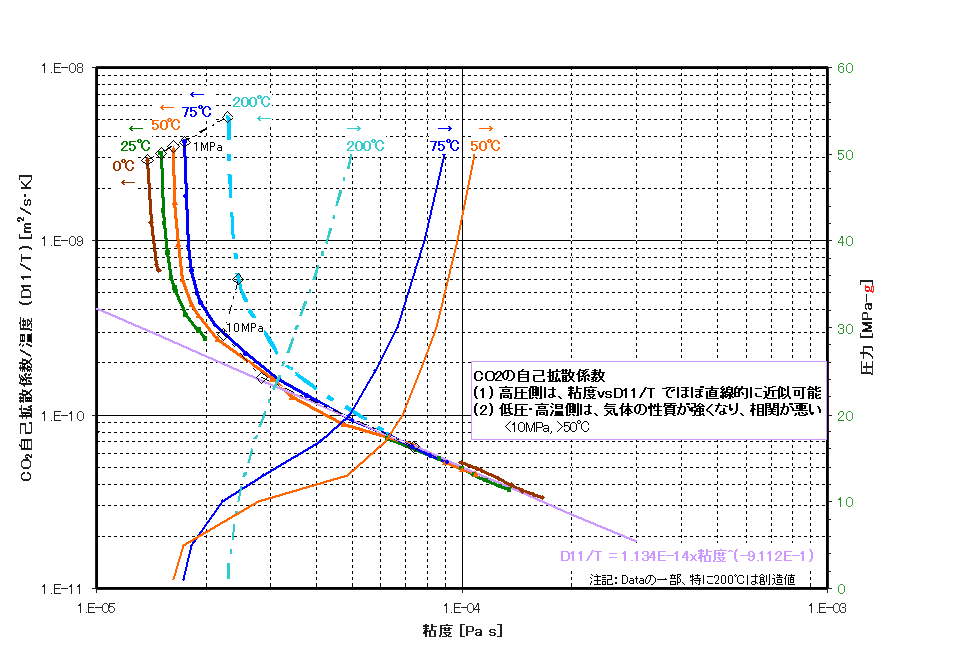
このデータをもとに、以下の推算式を作成しました。
D₁₁ / T [m²/(s K)] (下図の縦軸)
= 1.13388x10⁻¹⁴ x
粘度 [Pa s] ^ (-0.911161)
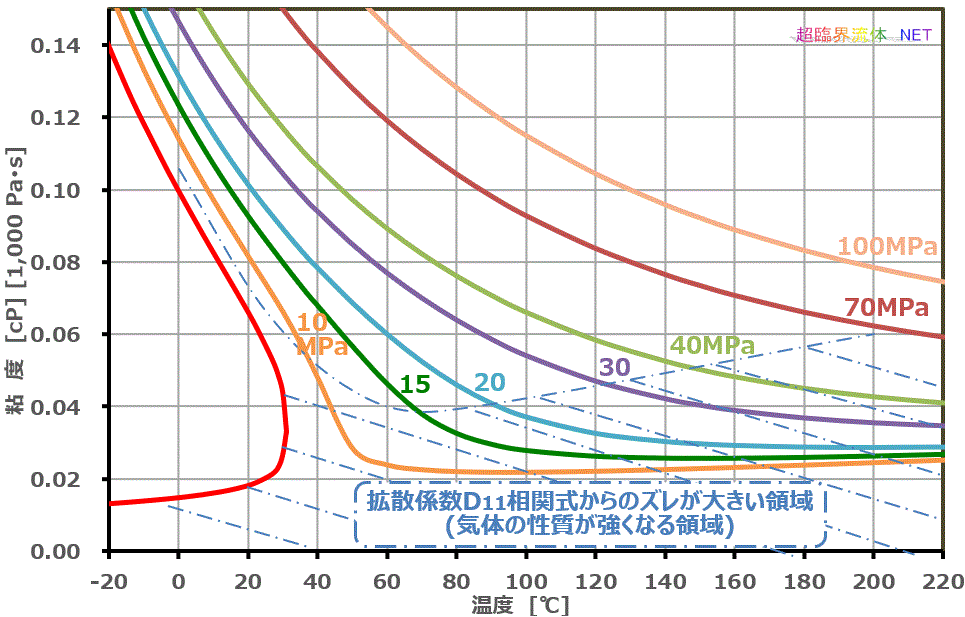
| 注記: | 348.15K(75℃)は、16MPa以下、323.15K(50℃)は、12MPa以下で相関式からのズレが大きくなります。ズレが大きくなる領域を右図に示します。これは、CO₂だけでなく、Xe,CH₄でも同様で、 粘性が小さくなると液体よりも気体の性質が強くなるためと考えられます。 |
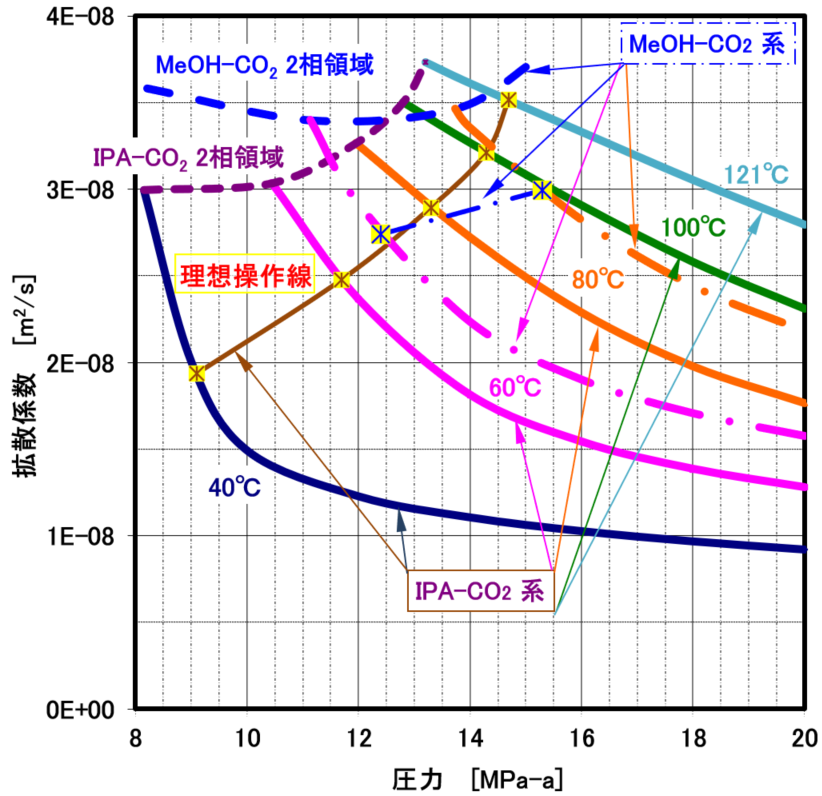
超臨界CO₂とメタノール(MeOH)、イソプロパノール(IPA)の各々の相互拡散係数のイメージを右図に示します。圧力が低く、温度が高い方が拡散係数は大きくなり、多孔質体内の物資移動速度が早くなります。二相領域を横切らない高相互拡散係数である理想操作線を図示しています。
アルコール乾燥の時の操作条件の決定時に非常に重要になります。詳細は、応用・適用分野の乾燥を参照下さい。
K = kf × Ap × (Cd - Cci)
K:物質移動係数 [kg/sec]、 kf:境膜物質移動係数 [m/s]、
Ap:界表面積 [m2]、 Cc - Cci:界面での濃度差 [kg/m3]
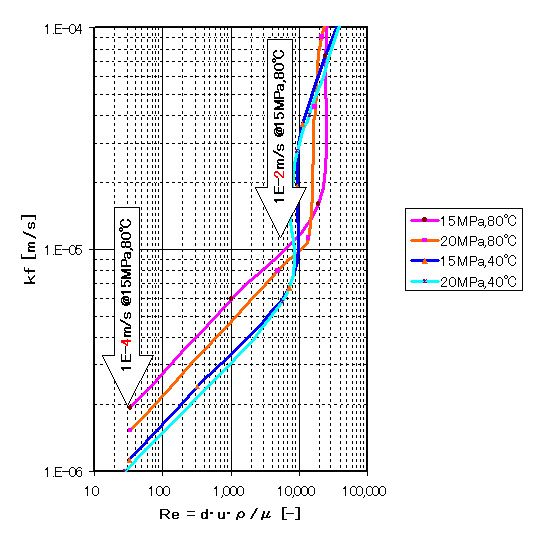
物質移動係数 kf は、これを溶質の拡散係数Deと流路の代表長さdとで無次元化したシャーウッド数Sh ≡ d・kc/Deで表現されます。レイノルズ数 Re に対する物質移動係数 kf の試算例を下図に示します。